CHEATING CLASS

Last Updated on June 17, 2022 by Ria Pathak

Concepts Used

Dynamic programming.

Difficulty Level

Medium.

Problem Statement :

Let’s suppose when a person i cheats from a person j, then we draw a line segment between them. We need to find the number of ways in which N people giving the exam(in a circular table) can cheat in pairs provided there is no crossover (Two lines intersecting each other).

Example:

n=4

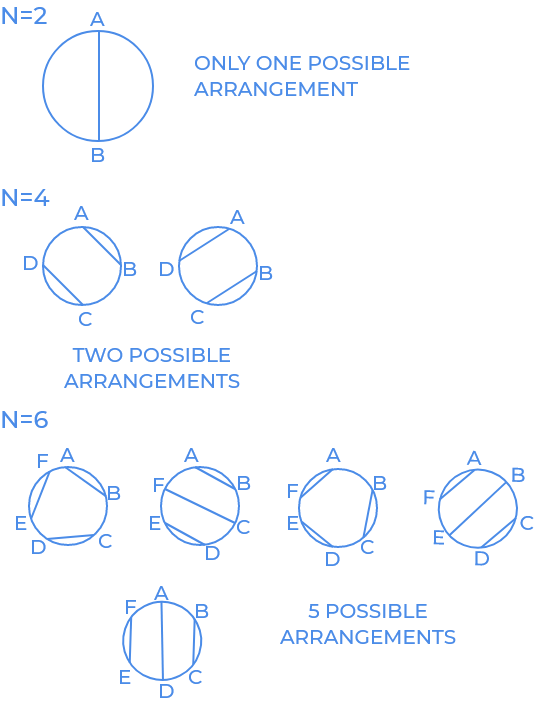
In the first sample provided above, there are 2 chords and 4 points. Let us label them as A, B, C, D in order. Now possible arrangements are chords AB and chords CD, the second possible arrangement is chord AD and chord BC.

Note: we can’t take chord AC and chord BD because the will intersect and we only have to consider non-intersecting chord.

Solving approach :

BRUTE FORCE :

Drawing a chord between any two points divides the circle into two sets s1 and s2 with x and n-x-2 points.
This again breaks the problem into two subproblems and so on.
This way we can derive a recurrence relation:
W(n) = sum[i = 0 to n-1] { W(i)W(n-i-1) }.

Brute force approach will take exponential time to calculate the required number of ways.But if we use recursion with memoization ,it can be achieved in O(N²) time.

You are encouraged to implement the above brute force and think of memoization on your own first ,before looking at the solution.
See original problem statement here

Optimization:

Before proceeding to the solution we can see that the recursive solution will take exponential time(without memoization) so we will proceed to the dynamic programming approach. In this approach, we select a point and a variable point and then make a chord using both points to divide the circle into two halves then using dp matrix we will find the number of ways to form rest of the chords in both halves multiply them and add them to the solution of ith column. We will proceed this with same fixed point and different variable point and store the answer in ith column.

Solutions:

 #include <stdio.h>

    #define ld long long
     int main() {
    ld dp[61];
    dp[0]=dp[1]=1;
    for(int i=2;i<61;i++)
    {
        dp[i]=0;
        for(int j=0;j<i;j++)
        {
            dp[i]+=dp[j]*dp[i-j-1];
        }
    }
    int t;
    scanf("%d",&t);
    for(;t>0;t--)
    {
        int n;
        scanf("%d",&n);
        n/=2;
        printf("%d\n",dp[n]);
    }
    return 0;
    }

#include<bits/stdc++.h>
      using namespace std;

      #define ld long long
      int main() {
      ld dp[61];
      dp[0]=dp[1]=1;
      for(int i=2;i<61;i++)
      {
        dp[i]=0;
        for(int j=0;j<i;j++)
        {
            dp[i]+=dp[j]*dp[i-j-1];
        }
      }
      int t;
      cin>>t;
      for(;t>0;t--)
      {
        int n;
        cin>>n;
        n/=2;
        cout<<dp[n]<<endl;
      }
       return 0;
       }

import java.util.*;
import java.io.*;
     class prepbytes { 
     static int chordCnt(int A) 
     { 
        int n = 2 * A;
        int[] dpArray = new int[n + 1]; 
        dpArray[0] = 1; 
        dpArray[2] = 1; 
        for (int i = 4; i <= n; i += 2) { 
            for (int j = 0; j < i - 1; j += 2)  
            { 
                dpArray[i] += (dpArray[j] *  
                              dpArray[i - 2 - j]); 
            } 
        } 

        // returning the required number 
        return dpArray[n]; 
      } 
      public static void main(String[] args) 
      { 
        Scanner sc = new Scanner(System.in);
        int t= sc.nextInt();
        while(t-- >0 ){
            int n = sc.nextInt();
        System.out.println(chordCnt(n/2)); 
        }
      } 
      } 

dp = [0 for i in range(61)]
dp[0]=dp[1]=1
for i in range(2, 61):

	dp[i] = 0

	for j in range(i):
		dp[i] += dp[j] * dp[i - j - 1]
	
for _ in range(int(input())):
	n = int(input())
	n //= 2
	print(dp[n])

Space complexity: O(N²)
[forminator_quiz id="2177"]

This article tried to discuss a dynamic problem by following the brute force approach. Hope this blog helps you understand the concept. To practice more problems on Dynamic programming you can check out MYCODE | Competitive Programming