Last Updated on March 28, 2022 by Ria Pathak

CONCEPTS USED:
Dynamic programming
DIFFICULTY LEVEL:
Hard
PROBLEM STATEMENT(SIMPLIFIED):
Himanshu visited a building with N floors and he carried with him k eggs, he found out that the eggs are rotten, so he plays a trick he wants to know the maximum floor from which the egg can be dropped without breaking the egg.
- An egg that survives the fall can be used again.
- A broken egg cannot be used again.
You know Himanshu is very lazy, help him find the minimum number of moves required to find the answer.- If egg breaks when dropped from some floor then it will break if dropped from any higher floor.
- If egg does not break when dropped from some floor then it will not break if dropped from any lower floor.
For Example :
2
30 4
6 2
5
3See original problem statement here
SOLVING APPROACH:
Recursion: try dropping an egg from each floor from 1 to n and calculate the minimum number of dropping needed in worst case.
Base case –
Eggs – 1, floors – x : play safe and drop from floor 1, if egg does not break then drop from floor 2 and so on. So in worst case x times an egg needs to be dropped to find the solution.
- Floors = 0: No trials are required.
- Floors = 1: 1 trails is required.
For rest of the case, if an egg is dropped from xth floor then there are only 2 outcomes which are possible. Either egg will break OR egg will not break.
- If Egg breaks – check the floors lower than x. So problem is reduced is
n-1eggs andx-1floors.- If egg does not break – check the floors higher than x floors with all the n eggs are remaining. So problem is reduced to n eggs and k-x floors.
getDrops (k,n) =
1 + Min(x = 1,2,….n) [(drops(k-1, n-1), drops(k, n-x)]Time Complexity: 2k
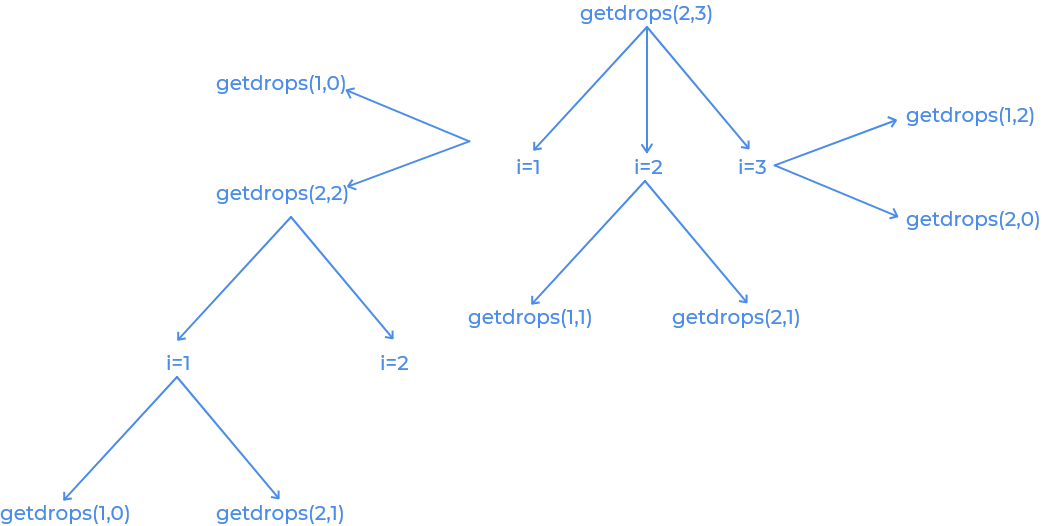
Now look at this recursion tree.We are solving many subproblems several times.
Dynamic Programming:
Bottom-up:
Solve it in bottom up manner, means start from the smallest sub problem possible (here it is 0 eggs 0 floors) and solve it. Store the result in some temporary storage.
Recursive equation will be same as above. Start solving from smallest sub problem and move towards final problem. Use the temporary result being stored instead of solving the sub problems again.
See the code for more understanding.
Time Complexity: nk2
#include <stdio.h>
int max(int x,int y)
{
if(x>y)return x;
return y;
}
int main()
{
//write your code here
int t;
scanf("%d",&t);
while(t--)
{
int n,e;
scanf("%d%d",&n,&e);
int dp[e+1][n+1];
for(int i=0;i<=n;i++)
dp[1][i]=i;
for(int i=1;i<=e;i++)
dp[i][1]=1;
for(int i=2;i<=e;i++)
{
for(int j=2;j<=n;j++)
{
dp[i][j]=1000000000;
for(int k=1;k<=j;k++)
{
int res=1+max(dp[i-1][k-1],dp[i][j-k]);
if(res<dp[i][j])
dp[i][j]=res;
}
}
}
printf("%d\n",dp[e][n]);
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
//write your code here
int t;
cin>>t;
while(t--)
{
int n,e;
cin>>n>>e;
int dp[e+1][n+1];
for(int i=0;i<=n;i++)
dp[1][i]=i;
for(int i=1;i<=e;i++)
dp[i][1]=1;
for(int i=2;i<=e;i++)
{
for(int j=2;j<=n;j++)
{
dp[i][j]=1000000000;
for(int k=1;k<=j;k++)
{
int res=1+max(dp[i-1][k-1],dp[i][j-k]);
if(res<dp[i][j])
dp[i][j]=res;
}
}
}
cout<<dp[e][n]<<"\n";
}
return 0;
}
import java.util.*;
import java.io.*;
class DropEgg {
static int max(int a, int b)
{
return (a > b) ? a : b;
}
static int eggDrop(int n, int k)
{
int eggFloor[][] = new int[n + 1][k + 1];
int res;
int i, j, x;
for (i = 1; i <= n; i++) {
eggFloor[i][1] = 1;
eggFloor[i][0] = 0;
}
for (j = 1; j <= k; j++)
eggFloor[1][j] = j;
for (i = 2; i <= n; i++) {
for (j = 2; j <= k; j++) {
eggFloor[i][j] = Integer.MAX_VALUE;
for (x = 1; x <= j; x++) {
res = 1 + max(
eggFloor[i - 1][x - 1],
eggFloor[i][j - x]);
if (res < eggFloor[i][j])
eggFloor[i][j] = res;
}
}
}
return eggFloor[n][k];
}
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int t= sc.nextInt();
while(t-- >0 ){
int n = sc.nextInt();
int k = sc.nextInt();
System.out.println( eggDrop(k, n)); }
}
}
EFFICIENT SOLUTION:
How many floors we can cover with
xtrials?When we drop an egg, two cases arise.
- If egg breaks, then we are left with
x-1trials andn-1eggs.- If egg does not break, then we are left with
x-1trials and n eggsLet
mf(x, n)be the maximum number of floors
that we can cover with x trials and n eggs. From above
two cases, we can write.
mf(x, n)=mf(x-1, n-1)+mf(x-1, n)+ 1
For all x >= 1 and n >= 1Base cases :
We can’t cover any floor with 0 trials or 0 eggs
mf(0, n)=0
mf(x, 0)=0Since we need to cover k floors,
mf(x, n)>=k———-(1)
maxFloors(x, n)= ∑xCi
1 <= i From above two equations, we can say.
∑xCj >=k
1 <= i <= n
Basically we need to find minimum value of x
that satisfies above inequality. We can find
such x using Binary Search.
#include <stdio.h>
int max(int x,int y)
{
if(x>y)return x;
return y;
}
int main()
{
//write your code here
int t;
scanf("%d",&t);
while(t--)
{
int n,e;
scanf("%d%d",&n,&e);
int dp[e+1][n+1];
for(int i=0;i<=n;i++)
dp[1][i]=i;
for(int i=1;i<=e;i++)
dp[i][1]=1;
for(int i=2;i<=e;i++)
{
for(int j=2;j<=n;j++)
{
dp[i][j]=1000000000;
for(int k=1;k<=j;k++)
{
int res=1+max(dp[i-1][k-1],dp[i][j-k]);
if(res<dp[i][j])
dp[i][j]=res;
}
}
}
printf("%d\n",dp[e][n]);
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
//write your code here
int t;
cin>>t;
while(t--)
{
int n,e;
cin>>n>>e;
int dp[e+1][n+1];
for(int i=0;i<=n;i++)
dp[1][i]=i;
for(int i=1;i<=e;i++)
dp[i][1]=1;
for(int i=2;i<=e;i++)
{
for(int j=2;j<=n;j++)
{
dp[i][j]=1000000000;
for(int k=1;k<=j;k++)
{
int res=1+max(dp[i-1][k-1],dp[i][j-k]);
if(res<dp[i][j])
dp[i][j]=res;
}
}
}
cout<<dp[e][n]<<"\n";
}
return 0;
}
import java.util.*;
import java.io.*;
class DropEgg {
static int max(int a, int b)
{
return (a > b) ? a : b;
}
static int eggDrop(int n, int k)
{
int eggFloor[][] = new int[n + 1][k + 1];
int res;
int i, j, x;
for (i = 1; i <= n; i++) {
eggFloor[i][1] = 1;
eggFloor[i][0] = 0;
}
for (j = 1; j <= k; j++)
eggFloor[1][j] = j;
for (i = 2; i <= n; i++) {
for (j = 2; j <= k; j++) {
eggFloor[i][j] = Integer.MAX_VALUE;
for (x = 1; x <= j; x++) {
res = 1 + max(
eggFloor[i - 1][x - 1],
eggFloor[i][j - x]);
if (res < eggFloor[i][j])
eggFloor[i][j] = res;
}
}
}
return eggFloor[n][k];
}
public static void main(String args[])
{
Scanner sc = new Scanner(System.in);
int t= sc.nextInt();
while(t-- >0 ){
int n = sc.nextInt();
int k = sc.nextInt();
System.out.println( eggDrop(k, n)); }
}
}
[forminator_quiz id=2170]
This article tried to discuss Dynamic programming. Hope this blog helps you understand and solve the problem. To practice more problems on Dynamic programming you can check out MYCODE | Competitive Programming.