Last Updated on March 28, 2022 by Ria Pathak

Concepts Used
Breadth First Search
Difficulty Level
Hard
Problem Statement :
Given a string , we are standing at the starting point and we have to reach end in minimum steps by following these rules:
- We can either jump to neighbour indices or,
- We can jump to a position with same value.
See original problem statement here
Solution Approach :
Introduction :
Idea is to consider every character index, as a vertex of a graph where there is an edge between next and previous indices (vertices) and also between the indices with same values.
Example : 1213 => string
By taking indices of the string as vertices, 0–2, 0–1, 1–0, 1–2, 2–3, these are the egdes of the graph. Notice there is a direct edge between 1 (at index 0) and 1(at index 2) as the values in the both indices are same.
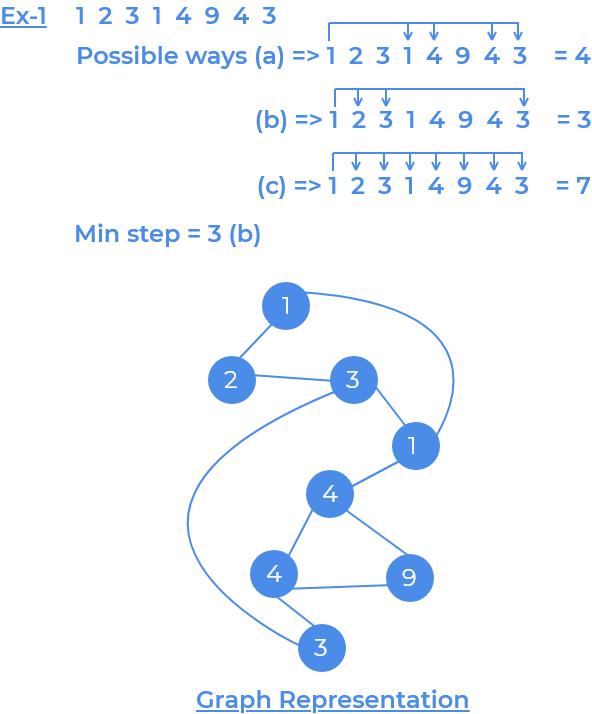
Description :
We can use bfs or breadth first search to traverse every vertex, as bfs guarantees the minimum steps (why?, since it moves level wise). As mentioned above we can make a graph with indices as vertices, with every adjacent index and index with same values, as an edge. Additionally, we can store the indices of every character, using a 2-D array with 10 rows (0-9) for values, where each row stores the index of the character with value same as row number.
We will use visited[] array to keep track of the indices which is already visited so we visit every vertex once only. Now we just have to traverse through all the vertices and for every vertex v store the distance of every adjacent vertex a using distance array distance[] as, distance[a]=distance[v]+1.
Algorithms :
minDistance() :
-
create a queue and push the current index now perform following operations untill the queue is empty:
-
each time we pop a vertex
vfrom queue, (v= queue.front() ), we will mark the vertexvas visited (visited[v]= true). -
Iterate for all the adjacent vertices of
vand for every adjacent vertexa, do following :-
mark
aas visited and update distance as,distance[a]= distance[v]+1. -
push
ainto the queue. -
if
ais not visited,
and ifparent[v] != a. -
update the ans ( ans = min(ans,current cycle length) ).
-
-
Now check if the previous and next index is visited or not, if not mark them as visited and push into the queue.
Complexity Analysis:
The time complexity of the above method is represented in the form of O(V+E), where V is the number of verices and E is the number of edges.
Solutions:
#include <stdio.h>
#include <stdlib.h>
#include<string.h>
#define INT_MIN -999999
//ADJACENCY LIST
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
};
// Create a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Create a graph
struct Graph* createAGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
int i;
for (i = 0; i < vertices; i++)
graph->adjLists[i] = NULL;
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int s, int d) {
// Add edge from s to d
struct node* newNode = createNode(d);
newNode->next = graph->adjLists[s];
graph->adjLists[s] = newNode;
}
//QUEUE
struct Queue
{
int front, rear, size;
unsigned capacity;
int* array;
};
struct Queue* createQueue(unsigned capacity)
{
struct Queue* queue = (struct Queue*) malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1; // This is important, see the enqueue
queue->array = (int*) malloc(queue->capacity * sizeof(int));
return queue;
}
int isEmpty(struct Queue* queue)
{ return (queue->size == 0); }
void enqueue(struct Queue* queue, int item)
{
if (isFull(queue))
return;
queue->rear = (queue->rear + 1)%queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
//printf("%d enqueued to queue\n", item);
}
int dequeue(struct Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
int item = queue->array[queue->front];
queue->front = (queue->front + 1)%queue->capacity;
queue->size = queue->size - 1;
return item;
}
// Function to get front of queue
int front(struct Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
return queue->array[queue->front];
}
// Function to get rear of queue
int rear(struct Queue* queue)
{
if (isEmpty(queue))
return INT_MIN;
return queue->array[queue->rear];
}
int getMinStepToReachEnd(int arr[], int N)
{
int visit[N];
int distance[N];
struct Graph * digit= createAGraph(10);
// In starting all index are unvisited
memset(visit, 0, sizeof(visit));
for (int i = 1; i < N; i++)
addEdge(digit, arr[i],i);
distance[0] = 0;
visit[0] = 1;
// Creating a queue and inserting index 0.
struct Queue* q = createQueue(1000);
enqueue(q,0);
// loop untill queue in not empty
while(!isEmpty(q))
{
// Get an item from queue, q.
int idx = front(q); dequeue(q);
// If we reached to last index break from loop
if (idx == N-1)
break;
// Find value of dequeued index
int d = arr[idx];
struct node * temp = digit->adjLists[d];
// looping for all indices with value as d.
//for (int i = 0; i<digit[d].size(); i++)
while(temp)
{
int nextidx = temp->vertex;
if (!visit[nextidx])
{
visit[nextidx] = 1;
enqueue(q,nextidx);
// update the distance of this nextidx
distance[nextidx] = distance[idx] + 1;
}
temp = temp->next;
}
// checking condition for previous index
if (idx-1 >= 0 && !visit[idx - 1])
{
visit[idx - 1] = 1;
enqueue(q,idx - 1);
distance[idx - 1] = distance[idx] + 1;
}
// checking condition for next index
if (idx + 1 < N && !visit[idx + 1])
{
visit[idx + 1] = 1;
enqueue(q,idx + 1);
distance[idx + 1] = distance[idx] + 1;
}
}
// N-1th position has the final result
return distance[N - 1];
}
int main()
{
char str[1000001];
scanf("%s",str);
int n = strlen(str);
int arr[n] ;
for(int i=0;i<n;i++)
{
arr[i]= str[i]-'0';
}
printf("%d\n",getMinStepToReachEnd(arr, n));
return 0;
}
#include<bits/stdc++.h>
using namespace std;
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
#define memo(a,v) memset(a,v,sizeof(a))
#define CLR(a) memo(a,0)
#define pb push_back
#define all(a) a.begin(),a.end()
#define eps (1e-9)
#define inf (1<<29)
#define i64 long long
#define u64 unsigned i64
#define AIN(a,b,c) (a<=b && b<=c)
int d[100005];
vector<int> adj[10];
char a[100005];
int main(){
int i, x, u, v, sz, n;
//while(scanf("%s",a)==1){
cin >> a;
for (i = 0; i < 10; i++)
adj[i].clear();
for (i = 0; a[i]; i++)
{
AIN('0', a[i], '9');
d[i] = -1;
// if(i && a[i-1]==a[i] && i<n-1 && a[i+1]==a[i]) continue;
adj[a[i] - '0'].pb(i);
}
AIN(1, i, 100000);
n = i;
queue<int> q;
q.push(0);
d[0] = 0;
while (!q.empty())
{
u = q.front();
if (u == n - 1)
break;
q.pop();
x = a[u] - '0';
sz = adj[x].size();
for (i = 0; i < sz; i++)
{
v = adj[x][i];
if (d[v] == -1)
{
d[v] = d[u] + 1;
q.push(v);
}
}
adj[x].clear();
if (u && d[u - 1] == -1) {
d[u - 1] = d[u] + 1;
q.push(u - 1);
}
if (d[u + 1] == -1) {
d[u + 1] = d[u] + 1;
q.push(u + 1);
}
}
assert(u == n - 1 && d[u] != -1);
cout << d[u] << endl;
//}
return 0;
}
import java.util.*;
class GFG
{
// Method returns minimum step
// to reach end of array
static int getMinStepToReachEnd(int arr[],
int N)
{
// visit boolean array checks whether
// current index is previously visited
boolean []visit = new boolean[N];
// distance array stores distance of
// current index from starting index
int []distance = new int[N];
// digit vector stores indices where a
// particular number resides
Vector<Integer> []digit = new Vector[10];
for(int i = 0; i < 10; i++)
digit[i] = new Vector<>();
// In starting all index are unvisited
for(int i = 0; i < N; i++)
visit[i] = false;
// storing indices of each number
// in digit vector
for (int i = 1; i < N; i++)
digit[arr[i]].add(i);
// for starting index distance will be zero
distance[0] = 0;
visit[0] = true;
// Creating a queue and inserting index 0.
Queue<Integer> q = new LinkedList<>();
q.add(0);
// loop untill queue in not empty
while(!q.isEmpty())
{
// Get an item from queue, q.
int idx = q.peek();
q.remove();
// If we reached to last
// index break from loop
if (idx == N - 1)
break;
// Find value of dequeued index
int d = arr[idx];
// looping for all indices with value as d.
for (int i = 0; i < digit[d].size(); i++)
{
int nextidx = digit[d].get(i);
if (!visit[nextidx])
{
visit[nextidx] = true;
q.add(nextidx);
// update the distance of this nextidx
distance[nextidx] = distance[idx] + 1;
}
}
// clear all indices for digit d,
// because all of them are processed
digit[d].clear();
// checking condition for previous index
if (idx - 1 >= 0 && !visit[idx - 1])
{
visit[idx - 1] = true;
q.add(idx - 1);
distance[idx - 1] = distance[idx] + 1;
}
// checking condition for next index
if (idx + 1 < N && !visit[idx + 1])
{
visit[idx + 1] = true;
q.add(idx + 1);
distance[idx + 1] = distance[idx] + 1;
}
}
// N-1th position has the final result
return distance[N - 1];
}
// Driver Code
public static void main(String []args)
{
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
int n = str.length();
int [] arr = new int[n];
for(int i =0 ;i<n;i++)
{
arr[i] = Character.getNumericValue(str.charAt(i));
}
System.out.println(getMinStepToReachEnd(arr, n));
}
}
[forminator_quiz id="1937"]
This article tried to discuss Breadth First Search. Hope this blog helps you understand and solve the problem. To practice more problems on Breadth First Search you can check out MYCODE | Competitive Programming.


