Last Updated on November 28, 2022 by Prepbytes

This blog will discuss an important problem of count pairs from two linked with given sum Such problems do come in interviews.
Before solving the problem, it’s recommended that a known basic traversal in the Linked List check Linked List.
In this blog, we dive deep into each detail to get a number of pairs from two linked lists whose sum is equal to a given value.
Let’s look at the problem statement of count pairs from two linked with given sum for a better understanding.
How to count pairs from two linked list with given sum
We will be given two linked lists and an integer target as input, and we need to count pairs of integers in both lists such that each element of the pair belongs to different lists and their sum is equal to the given target integer.
To understand the problem statement, let’s take an example.
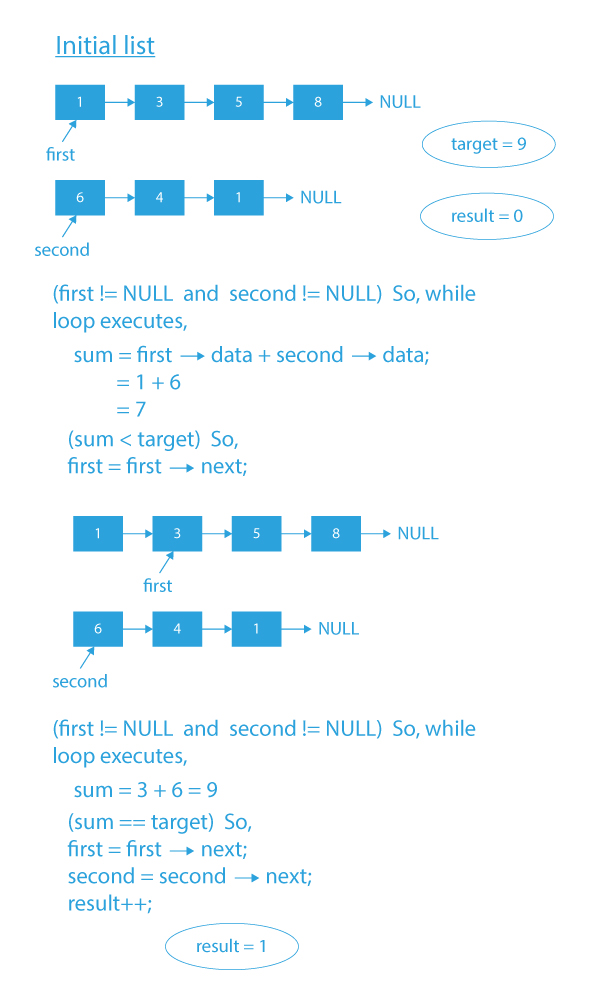
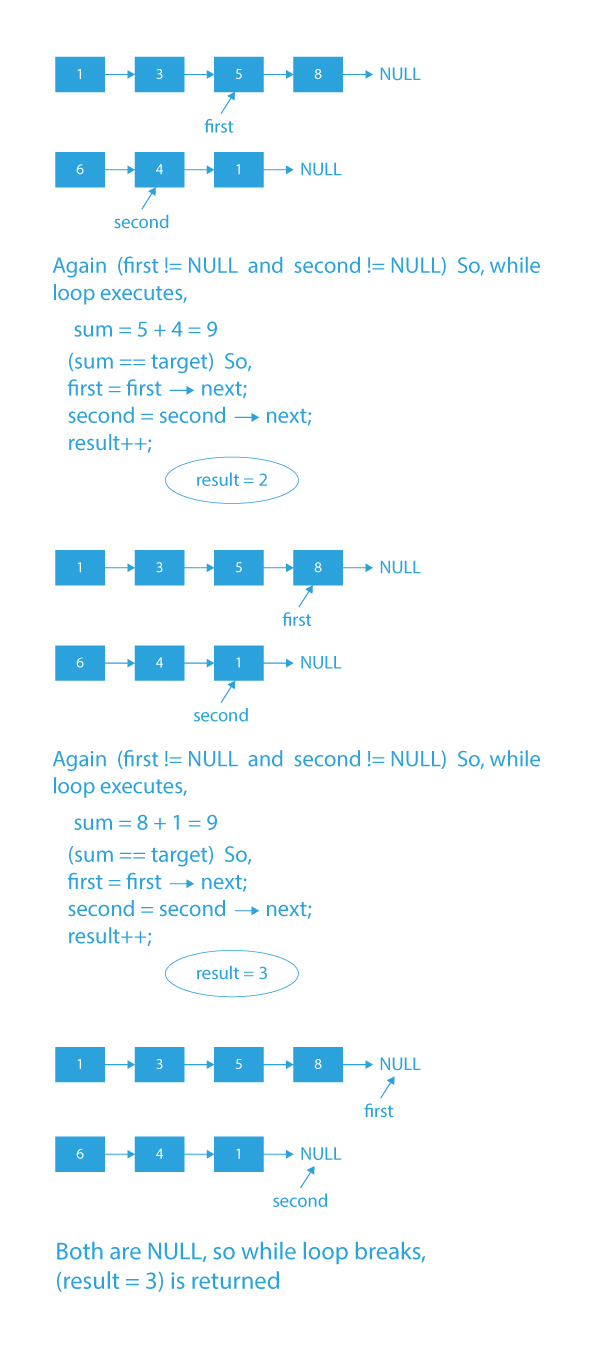
If the linked lists given to us are 1→3→5→8→NULL, 6→4→1→NULL, and the target = 9. Then, according to the problem statement:
- We need to find pairs of integers such that each element of the pair belongs to a different list, and their sum is equal to 9.
- All such pairs are – (3,6), (8,1) and (5,4)
- There are three possible pairs, so; we need to print 3 as output, i.e., the total count of possible pairs.
At this point, we have understood the problem statement. Now we will try to formulate an approach for this problem.
Before moving to the approach section, try to think about how you can approach this problem.
- If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.
Let’s move to the approach section.
Approach 1 of count pairs from two linked with given sum
The naive approach that comes to our mind is that first, select a node in the first list and for each selected node in the first list, iterate in the second list and check if the sum of node’s (selected node from first list + node from the second list) is equal to the target or not.
Time Complexity of count pairs from two linked with given sum: O(N2), N is the number of nodes in a list.
Space Complexity of count pairs from two linked with given sum: O(1)
The above approach gives the correct result, but its time complexity is high. Can we reduce the time complexity? Let us find out If we can do so in the below approach.
Approach 2 of count pairs from two linked with given sum
- In this approach, we store all elements of the first list in a HashSet.
- Then, we iterate on the elements of the second list and find if the difference in the value of the current element of the second list and target exists in hash or not.
- If it exists in the HashSet, then we will increase the count by one.
Algorithm of count pairs from two linked with given sum
- Initialize a result variable with 0 and create an unordered set.
- Push all elements of the first list in the set created above.
-
Run a while loop till head2 (pointer to the second list) is not NULL.
-
Check if (target – head2->data) exists in the set or not
- If it exists then, increment the result by one.
-
Move the pointer head2 forward by one node.
-
- After the loop is executed, return result from the function.
Code Implementation of count pairs from two linked with given sum
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
// function to insert a node at the
// beginning of the linked list
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list to the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
// function to count all pairs from both the linked
// lists whose sum is equal to a given value
int countPairs(struct Node* head1, struct Node* head2,
int x)
{
int count = 0;
// sort head1 in ascending order and
// head2 in descending order
// sort (head1), sort (head2)
// For simplicity both lists are considered to be
// sorted in the respective orders
// traverse both the lists from left to right
while (head1 != NULL && head2 != NULL)
{
// if this sum is equal to 'x', then move both
// the lists to next nodes and increment 'count'
if ((head1->data + head2->data) == x)
{
head1 = head1->next;
head2 = head2->next;
count++;
}
// if this sum is greater than x, then
// move head2 to next node
else if ((head1->data + head2->data) > x)
head2 = head2->next;
// else move head1 to next node
else
head1 = head1->next;
}
// required count of pairs
return count;
}
// Driver program to test above
int main()
{
struct Node* head1 = NULL;
struct Node* head2 = NULL;
// create linked list1 1->3->5->7
// assumed to be in ascending order
push(&head1, 7);
push(&head1, 5);
push(&head1, 3);
push(&head1, 1);
// create linked list2 8->5->3->2
// assumed to be in descending order
push(&head2, 2);
push(&head2, 3);
push(&head2, 5);
push(&head2, 8);
int x = 10;
int ans = countPairs(head1, head2, x);
printf("Count = %d",ans);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
class Node{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
int countPairs(Node* head1, Node* head2,int target)
{
int result = 0;
unordered_set<int> hash_set;
//insert all elements of first list in
//the hash set
while (head1 != NULL)
{
hash_set.insert(head1->data);
head1 = head1->next;
}
// iterate on each elements of second list
while (head2 != NULL)
{
//find if (target - currentData) exists
//in the hashset
if (hash_set.find(target - head2->data) != hash_set.end())
result++;
head2 = head2->next;
}
// return the result
return result;
}
int main(void){
Node* first = NULL;
first = new Node(1);
first->next = new Node(3);
first->next->next = new Node(5);
first->next->next->next = new Node(8);
Node* second = NULL;
second = new Node(6);
second->next = new Node(4);
second->next->next = new Node(1);
cout<<"Count of pairs having sum "<<9<<" are: ";
cout<<countPairs(first,second,9);
}
class Node
{
int data;
Node next;
Node(int data)
{
this.data=data;
}
}
public class CountParis
{
static int countPairs(Node first,Node second, int target)
{
int result = 0;
// iterate both lists
while (first != null && second != null)
{
//calculate 'sum'
int sum = first.data + second.data;
//if sum equals target, increase result by 1
//and move both pointers
if (sum == target)
{
first = first.next;
second = second.next;
result++;
}
// if sum is more than target, move
// second pointer
else if (sum > target)
second = second.next;
// else move first pointer
else
first = first.next;
}
// required count of pairs
return result;
}
public static void main(String[] args)
{
Node first=null;
first=new Node(1);
first.next=new Node(3);
first.next.next=new Node(5);
first.next.next.next=new Node(8);
Node second=new Node(6);
second.next=new Node(4);
second.next.next=new Node(1);
System.out.println("Count of pairs having sum 9 are:");
System.out.println(countPairs(first, second, 9));
}
}
class Node:
def __init__(self):
self.data = 0
self.next = None
def push(head_ref, new_data):
new_node =Node()
new_node.data = new_data
new_node.next = (head_ref)
(head_ref) = new_node
return head_ref
def countPairs(first, second, target):
result = 0
while first and second:
sum = first.data + second.data
if sum == target:
first = first.next
second = second.next
result += 1
elif sum > target:
second = second.next
else:
first = first.next
return result
if __name__=='__main__':
head1 = None
head2 = None
head1 = push(head1, 1)
head1 = push(head1, 3)
head1 = push(head1, 5)
head1 = push(head1, 8)
head2 = push(head2, 6)
head2 = push(head2, 4)
head2 = push(head2, 1)
head2 = push(head2, 9)
x = 9
print("Count of pairs having sum", x,"are:", countPairs(head1, head2, x))
Output
Count of pairs having sum 9 are: 3Time Complexity of count pairs from two linked with given sum: O(n), n is the number of nodes in a list.
Space Complexity of count pairs from two linked with given sum: O(n), n is the number of nodes in a list.
In the above approach, we are using extra space to store the elements in a hash set. Can we reduce the extra space used? Let us find out If we can do so in the below approach.
Approach 3 of count pairs with given sum
- At first, we need to sort the first list in ascending order and the second list in descending order.
- The above step is performed so that we can predict whether moving forward in the lists is going to increase our current sum or decrease it.
- It is evident that moving forward in the first list is going to increase the pair sum, and moving forward in the second one is going to decrease it.
- Now, we will initialize two different pointers at the head of both lists.
- We will compute the sum pointed by the pointers in each step, and If the sum is equal to the target, we will increase our result by one and move both pointers simultaneously.
- If the sum is less than the target, we need to increase it so we will move the pointer of the first list forward by one node.
- Else, we will move the pointer of the second list by one node.
Algorithm count pairs with given sum
- Sort the first list in ascending order and the second list in descending order.
- Initialize a variable result by 0.
- Run a while loop till any one of first or second becomes NULL.
- Calculate sum as the sum of data of nodes pointed by first and second pointers.
- If the sum is equal to the target, increase the result by one and move both pointers forward by one node.
- If the sum is greater than the target, move the second pointer forward by one node.
- Else, move the first pointer forward by one node.
Note: For simplicity, in dry run and code implementation, we took the first and the second linked lists, which are already sorted in ascending and descending order, respectively. If you want to know how to sort a linked list, please feel free to refer to this article for sorting related concepts of linked list. Also, inside the code implementation, we haven’t provided the sorting function (function to sort the linked list); if you want to take unsorted linked lists, please sort them in proper format (the first list will be sorted in ascending order and the second list in descending order) using code from the above-mentioned article, before passing them to countPairs() function in the code.
Also, note that to sort a linked list in descending order, you can first sort the linked list in ascending order, and then you can reverse the sorted linked list.
Dry Run of count pairs from two linked with given sum
Code Implementation of count pairs from two linked with given sum
#include#include #include struct Node { int data; struct Node* next; }; /* Function to print nodes in a given linked list */ void printList(struct Node* node) { while (node != NULL) { printf("%d ", node->data); node = node->next; } } // The main function that // takes an array of lists // arr[0..last] and generates // the sorted output struct Node* mergeKLists(struct Node* arr[], int last) { // Traverse form second list to last for (int i = 1; i <= last; i++) { while (true) { // head of both the lists, // 0 and ith list. struct Node *head_0 = arr[0], *head_i = arr[i]; // Break if list ended if (head_i == NULL) break; // Smaller than first element if (head_0->data >= head_i->data) { arr[i] = head_i->next; head_i->next = head_0; arr[0] = head_i; } else // Traverse the first list while (head_0->next != NULL) { // Smaller than next element if (head_0->next->data >= head_i->data) { arr[i] = head_i->next; head_i->next = head_0->next; head_0->next = head_i; break; } // go to next node head_0 = head_0->next; // if last node if (head_0->next == NULL) { arr[i] = head_i->next; head_i->next = NULL; head_0->next = head_i; head_0->next->next = NULL; break; } } } } return arr[0]; } // Utility function to create a new node. struct Node* newNode(int data) { struct Node *temp = (struct Node *) malloc(sizeof(struct Node)); temp->data = data; temp->next = NULL; return temp; } // Driver program to test // above functions int main() { // Number of linked lists int k = 3; // Number of elements in each list int n = 4; // an array of pointers storing the // head nodes of the linked lists struct Node* arr[k]; arr[0] = newNode(10); arr[0]->next = newNode(30); arr[0]->next->next = newNode(50); arr[0]->next->next->next = newNode(70); arr[1] = newNode(20); arr[1]->next = newNode(40); arr[1]->next->next = newNode(60); arr[1]->next->next->next = newNode(80); arr[2] = newNode(0); arr[2]->next = newNode(90); arr[2]->next->next = newNode(100); arr[2]->next->next->next = newNode(11); // Merge all lists struct Node* head = mergeKLists(arr, k - 1); printList(head); return 0; }
#include<bits/stdc++.h>
using namespace std;
class Node{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
int countPairs(Node* first, Node* second,int target)
{
int result = 0;
// iterate both lists
while (first != NULL && second != NULL)
{
//calculate 'sum'
int sum = first->data + second->data;
//if sum equals target, increase result by 1
//and move both pointers
if (sum == target)
{
first = first->next;
second = second->next;
result++;
}
// if sum is more than target, move
// second pointer
else if (sum > target)
second = second->next;
// else move first pointer
else
first = first->next;
}
// required count of pairs
return result;
}
int main(void){
Node* first = NULL;
first = new Node(1);
first->next = new Node(3);
first->next->next = new Node(5);
first->next->next->next = new Node(8);
Node* second = NULL;
second = new Node(6);
second->next = new Node(4);
second->next->next = new Node(1);
cout<<"Count of pairs having sum "<<9<<" are: ";
cout<<countPairs(first,second,9);
}
import java.util.*;
class Node
{
int data;
Node next;
Node(int data)
{
this.data=data;
}
}
public class CountParis
{
static int countPairs(Node head1,Node head2, int target)
{
int res=0;
HashSet<Integer> h=new HashSet<>();
while(head1!=null)
{
h.add(head1.data);
head1=head1.next;
}
while(head2!=null)
{
if(h.contains(target-head2.data))
{
res++;
}
head2=head2.next;
}
return res;
}
public static void main(String[] args)
{
Node first=null;
first=new Node(1);
first.next=new Node(3);
first.next.next=new Node(5);
first.next.next.next=new Node(8);
Node second=new Node(6);
second.next=new Node(4);
second.next.next=new Node(1);
System.out.println("Count of pairs having sum 9 are:");
System.out.println(countPairs(first, second, 9));
}
}
class Node:
def __init__(self):
self.data = 0
self.next = None
def push(head_ref, new_data):
new_node =Node()
new_node.data = new_data
new_node.next = (head_ref)
(head_ref) = new_node
return head_ref
def countPairs(head1, head2, x):
count = 0
us = set()
# add all the elements of 1st list
# in the hash table(unordered_set 'us')
while (head1 != None):
us.add(head1.data)
# move to next node
head1 = head1.next
# iterate on each element of 2nd list
while (head2 != None):
# find (x - head2.data) in 'us'
if ((x - head2.data) in us):
count += 1
# move to next node
head2 = head2.next
# return the count
return count
if __name__=='__main__':
head1 = None
head2 = None
head1 = push(head1, 1)
head1 = push(head1, 3)
head1 = push(head1, 5)
head1 = push(head1, 8)
head2 = push(head2, 6)
head2 = push(head2, 4)
head2 = push(head2, 1)
head2 = push(head2, 9)
x = 9
print("Count of pairs having sum", x,"are:", countPairs(head1, head2, x))
Output
Count of pairs having sum 9 are: 3Time Complexity of count pairs from two linked with given sum: O(N log N), N is the number of nodes in the list
Space Complexity of count pairs from two linked with given sum: O(1)
Conclusion
So, this article taught us how to solve the problem of data structure, i.e., count pairs from two linked lists whose sum is equal to a given value. We also saw how to approach the problem using a naive approach followed by two efficient solutions. We discussed an iterative implementation and some basic traversal in linked lists using examples, pseudocode, and code in detail. If you want to solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs related to count pairs from two linked with given sum
1. What are the advantages of a linked list?
Some advantages of the linked list are as follows:
- Insertion and deletion operations can be implemented very easily, and these are not costly as they do not require the shifting of elements.
- They are dynamic. Hence, we can change their size whenever required.
- Stacks and queues can be implemented very easily using Linked Lists.
2. How does merge sort for linked list work?
The merge sort algorithm is a divide and conquers algorithm it divides the list into smaller sublists until each sublist contains only a single element, and a list of size one is always sorted; using this property, it merges two sorted sublists into a single sorted list.
3. Can we use two pointer approach without sorting the lists?
No, Because in the unsorted list we can’t decide whether its next element is greater or less than the current element. So we don’t move our pointer to increase or decrease the sum.


