Last Updated on July 27, 2023 by Mayank Dham

Linked lists consist of interconnected nodes, with each node containing data and a pointer to the next node in the sequence. Removing the middle node of a linked list poses a significant challenge. Here, we will discuss how to delete middle of linked list in an efficient way.
How to Delete the Middle Node of a Linked List?
The example given below will help in understanding the concept to delete middle element of linked list.
Input:

Since we have to delete middle element of linked list such that the resultant linked list after deletion will be like as shown in the output below.
Output:

Explanation:
Now, in the above given linked list, 3rd node is the middle node of the linked list. Since we have to delete middle element of linked list, we remove the node containing 10 as the data. After deleting the node, we get the final linked list as given below.

Here we have just made a connection between node(5) and node(15).
Things to observe about the deletion of nodes in a linked list
- If we take some more examples, we will notice that we need access to the previous and the next node of the node that we wish to delete. So, that we can connect the previous node to the next node
Say, if the deleted node is the target, its previous node is prev and its next node is next1. So, to do the deletion of the target node from the linked list, we need to do the following operations:
- prev→next = next1
- And finally free the target node
Similarly, in this problem, we need to first find the position of the middle node and node previous to the middle node and then following the above-mentioned steps of deletion we have to delete the middle element of the linked list.
So now we will see how to get the middle node and which node will be the middle node of the linked list in case of even length and odd length linked list.
Observations for the position of the middle element of linked list
Even Length Linked List:
- If there are an even number of nodes in the linked list, there will be two middle nodes. From these two middle nodes, we need to delete the second middle node of the linked list.
- For example, if the given linked list is 5→10→15→20→25→30, then 15 and 20 will be the two middle nodes of the linked list, and we will remove the second middle node which is 20.
- So our final modified linked list after deletion will look like this 5→10→15→25→30.
Odd Length Linked List:
If there are an odd number of nodes in the linked list, there will be a single middle node, and we will delete that node from the linked list.
For example, if the given linked list is 5→10→15→20→25, then 15 will be the middle node of the linked list, and we will remove this node from the linked list.
So our final modified linked list after deletion will look like this 5→10→20→30.
Note: If there is just one node present in the input linked list, that node should be removed and a new head should be returned.
Naive Approach to Delete the Middle Node of a Linked List
The naive approach to deleting the middle node is to count the number of nodes N in a linked list first, then delete the (N/2)th node using the simple deletion method.
The (N/2)th node is the middle node of the linked list.
Algorithm of Naive Approach to Delete the Middle Node of a Linked List
The algorithm for the above-mentioned Approach is given below.
-
If the head is NULL, return NULL.
-
If the next of head is NULL, delete the head and return NULL.
-
Create a node Head_copy and make it point to the head.
-
Initialize a counter variable count = 0, and now with help of head, traverse the linked list incrementing the count variable by 1 for each node of the linked list.
-
Finally, when the traversal of the list will be over count will contain the count of the number of nodes in the linked list.
-
The position of the middle node of the linked list will be given by (count/2), store it in a variable mid.
-
Now starting from the head of the linked list, traverse until the below condition holds:
while (mid-- > 1) { head = head→next; } -
At the end of the while loop, you will be at the node previous of the middle node. So now make head→next = head→next→next to delete the middle node of the linked list.
-
Finally, return Head_copy, which is the head of the newly formed list.
Code Implementation to Delete Middle Element of Linked List (By Using the Naive Approach)
The code to delete middle element in linked list in C, C++, Java, and Python is given below.
#include<stdio.h>
#include<stdlib.h>
struct Node {
int val;
struct Node* next;
};
// counting the number of nodes present in the list
int count_nodes(struct Node* head)
{
int n_count = 0;
while (head != NULL) {
head = head->next;
n_count++;
}
return n_count;
}
// returns head of the newly formed list
// after deleting the middle element.
struct Node* delete_middle(struct Node* head)
{
if (head == NULL)
return NULL;
if (head->next == NULL) {
free(head);
return NULL;
}
struct Node* Head_copy = head;
// total nodes currently there in the list
int count = count_nodes(head);
// position of middle element in the list
int mid = count / 2;
// Delete the middle node
while (mid-- > 1) {
head = head->next;
}
// Delete the middle node
head->next = head->next->next;
return Head_copy;
}
// Function to display the list
void display_List(struct Node* x)
{
while (x != NULL) {
printf("%d ->", x->val);
x = x->next;
}
// Last element points to null
printf("NULL\n");
}
// function to create a new node.
struct Node* newNode(int value)
{
struct Node* t = (struct Node*)malloc(sizeof(struct Node));
t->val = value;
t->next = NULL;
return t;
}
// Driver Function
int main()
{
// Adding elements to the empty list
struct Node* head = newNode(5);
head->next = newNode(10);
head->next->next = newNode(15);
head->next->next->next = newNode(20);
head->next->next->next->next = newNode(25);
printf("Original List\n");
display_List(head);
head = delete_middle(head);
printf("List after deleting the middle element\n");
display_List(head);
return 0;
}
// Program to delete middle element of a linked list
#include <bits stdc++.h>
using namespace std;
// Node in a linked list
struct Node {
int val;
struct Node* next;
};
// counting the number of nodes present in the list
int count_nodes(struct Node* head)
{
int n_count = 0;
while (head != NULL) {
head = head->next;
n_count++;
}
return n_count;
}
// returns head of the newly formed list
// after deleting the middle element.
struct Node* delete_middle(struct Node* head)
{
if (head == NULL)
return NULL;
if (head->next == NULL) {
delete head;
return NULL;
}
struct Node* Head_copy = head;
// total nodes currently there in the list
int count = count_nodes(head);
// position of middle element in the list
int mid = count / 2;
// Delete the middle node
while (mid-- > 1) {
head = head->next;
}
// Delete the middle node
head->next = head->next->next;
return Head_copy;
}
// Function to display the list
void display_List(struct Node* x)
{
while (x != NULL) {
cout << x->val << "->";
x = x->next;
}
// Last element points to null
cout << "NULL\n";
}
// function to create a new node.
Node* newNode(int value)
{
struct Node* t = new Node;
t->val = value;
t->next = NULL;
return t;
}
// Driver Function
int main()
{
// Adding elements to the empty list
struct Node* head = newNode(5);
head->next = newNode(10);
head->next->next = newNode(15);
head->next->next->next = newNode(20);
head->next->next->next->next = newNode(25);
cout << "Original List" << endl;
display_List(head);
head = delete_middle(head);
cout << "List after deleting the middle element"<< endl;
display_List(head);
return 0;
}
class DeleteMiddle {
/* Link list Node */
static class Node {
int data;
Node next;
}
// Utility function to create a new node.
static Node newNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.next = null;
return temp;
}
// count of nodes
static int countOfNodes(Node head)
{
int count = 0;
while (head != null) {
head = head.next;
count++;
}
return count;
}
static Node deleteMid(Node head)
{
if (head == null)
return null;
if (head.next == null) {
return null;
}
Node copyHead = head;
int count = countOfNodes(head);
// Find the middle node
int mid = count / 2;
// Delete the middle node
while (mid-- > 1) {
head = head.next;
}
// Delete the middle node
head.next = head.next.next;
return copyHead;
}
// A utility function to print a given linked list
static void printList(Node ptr)
{
while (ptr != null) {
System.out.print(ptr.data + "->");
ptr = ptr.next;
}
System.out.println("NULL");
}
/* Driver code*/
public static void main(String[] args)
{
/* Start with the empty list */
Node head = newNode(5);
head.next = newNode(10);
head.next.next = newNode(15);
head.next.next.next = newNode(20);
head.next.next.next.next = newNode(25);
System.out.println("Given Linked List");
printList(head);
head = deleteMid(head);
System.out.println(
"Linked List after deletion of middle");
printList(head);
}
}
# Node in a linked list
class Node:
def __init__(self):
self.data = 0
self.next = None
# counting the number of nodes present in the list
def countOfNodes(head):
count = 0
while (head != None):
head = head.next
count += 1
return count
# returns head of the newly formed list
# after deleting the middle element.
def deleteMid(head):
if (head == None):
return None
if (head.next == None):
del head
return None
copyHead = head
# after deleting the middle element.
count = countOfNodes(head)
# Find the middle node
mid = count // 2
# Delete the middle node
while (mid > 1):
mid -= 1
head = head.next
# Delete the middle node
head.next = head.next.next
return copyHead
# Function to display the list
def printList(ptr):
while (ptr != None):
print(ptr.data, end = '->')
ptr = ptr.next
print('NULL')
# function to create a new node.
def newNode(data):
temp = Node()
temp.data = data
temp.next = None
return temp
# Driver Code
if __name__=='__main__':
# Start with the empty list
head = newNode(5)
head.next = newNode(10)
head.next.next = newNode(15)
head.next.next.next = newNode(20)
head.next.next.next.next = newNode(25)
print("Given Linked List")
printList(head)
head = deleteMid(head)
print("Linked List after deletion of middle")
printList(head)
Output
Original List
5→10→15→20→25→NULL
List after deleting the middle element
5→10→20→25→NULLTime Complexity: O(n), as we are traversing the linked list only twice.
Space Complexity: O(1), No extra space is needed.
In the above-mentioned naive approach, we are traversing the linked list twice:
- First traversal to find the length of the linked list
- Then, in the second traversal, moving up to (length/2)th node of the linked list and delete it.
The first question we should ask ourselves is that do we actually need to find the length of the linked list to delete the middle node of the linked list.
The answer is No, we don’t need to find the length of the linked list to delete the middle node of the linked list.
Optimized Approach to Delete Middle Element of Linked List
Now in this approach, we will try to find the middle of the linked list in one traversal. We will see how can we tackle this:
- What if we start by taking two pointers, say slow and fast, and make both of them point to head initially.
- Now what will happen if we make a slow jump in one place and a fast jump in two places (fast moving with twice as speed as slow).
- If we notice carefully by doing the above steps, we will see that when the fast will reach the end of the list, the slow will be pointing to the middle of the list.
- With help of this technique, we can reach the middle of the linked list in one single pass, and hence our objective of reaching the middle of the linked list and deleting it will be achieved in one single traversal of the list. This technique is known as the double-pointer method.
The reason why slow will be pointing to the middle of the linked list when fast reaches the end is that, as our slow pointer is travelling with half of the speed of the fast pointer. When the fast pointer will reach the end of the linked list, till that time slow pointer will have travelled only half the distance travelled by the fast pointer and hence it will be in the middle of the linked list.
So in this way, using slow and fast pointers, we can find the position of the middle element of the linked list and then using its previous node we can delete the middle node of the linked list.
Algorithm of Optimized Approach to Delete Middle of Linked List
The algorithm is given below.
-
Create two-pointers, slow and fast.
-
We will also create a temporary pointer prev which will keep track of the previous node of the slow pointer.
-
Initially, both slow and fast will be pointing to the head of the linked list.
-
Now make the slow pointer jump one place and the fast pointer jump two places. The pointer will move further till the fast pointer reaches the end of the linked list.
-
When the fast pointer reaches the end, the slow pointer will be pointing to the middle of the linked list.
-
Now using the prev pointer which is keeping track of the previous node to the node pointed by the slow pointer, remove the node pointed by slow from the linked list by performing the below operations:
1) prev→next = slow->next
2) delete(slow) -
Finally, the middle node has been deleted from the linked list and we return the head of the linked list.
Dry Run to Delete Middle of Linked List
The dry run to delete middle element in linked list using the optimized approach is given below for a better understanding of the algorithm.
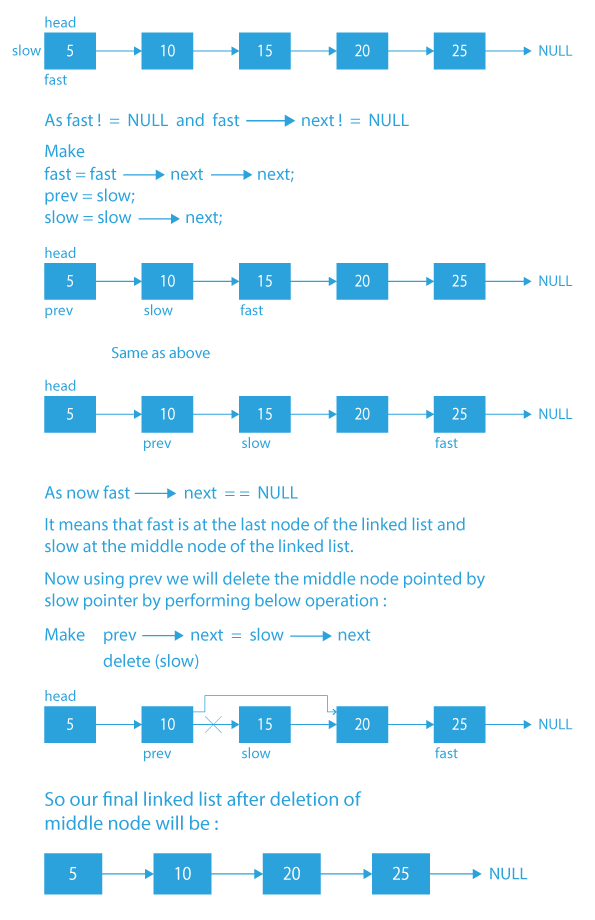
Code Implementation to Delete Middle Element of Linked List (Using Optimized Approach)
#include<stdio.h>
#include<stdlib.h>
struct Node {
int val;
struct Node* next;
};
// counting the number of nodes present in the list
int count_nodes(struct Node* head)
{
int n_count = 0;
while (head != NULL) {
head = head->next;
n_count++;
}
return n_count;
}
// returns head of the newly formed list
// after deleting the middle element.
struct Node* delete_middle(struct Node* head)
{
if (head == NULL)
return NULL;
if (head->next == NULL) {
free(head);
return NULL;
}
struct Node* Head_copy = head;
// total nodes currently there in the list
int count = count_nodes(head);
// position of middle element in the list
int mid = count / 2;
// Delete the middle node
while (mid-- > 1) {
head = head->next;
}
// Delete the middle node
head->next = head->next->next;
return Head_copy;
}
// Function to display the list
void display_List(struct Node* x)
{
while (x != NULL) {
printf("%d ->", x->val);
x = x->next;
}
// Last element points to null
printf("NULL\n");
}
// function to create a new node.
struct Node* newNode(int value)
{
struct Node* t = (struct Node*)malloc(sizeof(struct Node));
t->val = value;
t->next = NULL;
return t;
}
// Driver Function
int main()
{
// Adding elements to the empty list
struct Node* head = newNode(5);
head->next = newNode(10);
head->next->next = newNode(15);
head->next->next->next = newNode(20);
head->next->next->next->next = newNode(25);
printf("Original List\n");
display_List(head);
head = delete_middle(head);
printf("List after deleting the middle element\n");
display_List(head);
return 0;
}
// Program to delete middle element of a linked list
#include <bits stdc++.h>
using namespace std;
// Node in a linked list
struct Node {
int val;
struct Node* next;
};
// returns head of the newly formed list
// after deleting the middle element.
struct Node* delete_middle(struct Node* head)
{
if (head == NULL)
return NULL;
if (head->next == NULL) {
delete head;
return NULL;
}
// Inorder to reach the middle element,
// Initializing slow and fast pointers
struct Node* slow = head;
struct Node* fast = head;
// Finding out the middle as well as
// previous of middle.
// Store previous of slow
struct Node* prev;
while (fast != NULL && fast->next != NULL) {
fast = fast->next->next;
prev = slow;
slow = slow->next;
}
// Now, delete the middle element
prev->next = slow->next;
delete slow;
return head;
}
// Function to display the list
void display_List(struct Node* x)
{
while (x != NULL) {
cout << x->val << "->";
x = x->next;
}
// Last element points to null
cout << "NULL\n";
}
// function to create a new node.
Node* newNode(int value)
{
struct Node* t = new Node;
t->val = value;
t->next = NULL;
return t;
}
// Driver Function
int main()
{
// Adding elements to the empty list
struct Node* head = newNode(5);
head->next = newNode(10);
head->next->next = newNode(15);
head->next->next->next = newNode(20);
head->next->next->next->next = newNode(25);
cout << "Original List" << endl;
display_List(head);
head = delete_middle(head);
cout << "List after deleting the middle element"<< endl;
display_List(head);
return 0;
}
class DeleteMiddle {
/* Link list Node */
static class Node {
int data;
Node next;
}
// Deletes middle node and returns head of the modified list
static Node deleteMid(Node head)
{
// Base cases
if (head == null)
return null;
if (head.next == null) {
return null;
}
// Initialize slow and fast pointers to reach middle of linked list
Node slow_ptr = head;
Node fast_ptr = head;
// Find the middle and previous of middle.
Node prev = null;
// To store previous of slow_ptr
while (fast_ptr != null && fast_ptr.next != null) {
fast_ptr = fast_ptr.next.next;
prev = slow_ptr;
slow_ptr = slow_ptr.next;
}
// Delete the middle node
prev.next = slow_ptr.next;
return head;
}
// A utility function to print a given linked list
static void printList(Node ptr)
{
while (ptr != null) {
System.out.print(ptr.data + "->");
ptr = ptr.next;
}
System.out.println("NULL");
}
// Utility function to create a new node.
static Node newNode(int data)
{
Node temp = new Node();
temp.data = data;
temp.next = null;
return temp;
}
/* Driver code*/
public static void main(String[] args)
{
/* Start with the empty list */
Node head = newNode(1);
head.next = newNode(2);
head.next.next = newNode(3);
head.next.next.next = newNode(4);
System.out.println("Given Linked List");
printList(head);
head = deleteMid(head);
System.out.println("Linked List after deletion of middle");
printList(head);
}
}
# Node in a linked list
class Node:
def __init__(self, data):
self.data = data
self.next = None
# Create and handle list operations
class LinkedList:
def __init__(self):
# Head of the list
self.head = None
# Add new node to the list end
def addToList(self, data):
newNode = Node(data)
if self.head is None:
self.head = newNode
return
last = self.head
while last.next:
last = last.next
last.next = newNode
# Returns the list in string format
def __str__(self):
linkedListStr = ""
temp = self.head
while temp:
linkedListStr += str(temp.data) + "->"
temp = temp.next
return linkedListStr + "NULL"
# Method deletes middle node
def deleteMid(self):
# Base cases
if (self.head is None or
self.head.next is None):
return
# Initialize slow and fast pointers
# to reach middle of linked list
slow_Ptr = self.head
fast_Ptr = self.head
# Find the middle and previous of middle
prev = None
# To store previous of slow pointer
while (fast_Ptr is not None and
fast_Ptr.next is not None):
fast_Ptr = fast_Ptr.next.next
prev = slow_Ptr
slow_Ptr = slow_Ptr.next
# Delete the middle node
prev.next = slow_Ptr.next
# Driver code
linkedList = LinkedList()
linkedList.addToList(5)
linkedList.addToList(10)
linkedList.addToList(15)
linkedList.addToList(20)
linkedList.addToList(25)
print("Original List")
print(linkedList)
linkedList.deleteMid()
print("List after deleting the middle element")
print(linkedList)
Output
Original List
5→10→15→20→25→NULL
List after deleting the middle element
5→10→20→25→NULLTime Complexity: O(n), only a single traversal of the linked list is required.
Space Complexity: O(1), as no extra space is being used to delete middle element of linked list.
Conclusion
In this article, we learned about how to delete the middle element of the linked list. First, we used the naive approach in which we first count the total number of nodes in the linked list and then delete the (N/2)th node. This approach required 2 traversals. Next, we discussed the optimized approach which used the concept of slow and fast pointers to find the middle element and then deleted the
Frequently Asked Questions(FAQs) related to delete the middle node of linked list
Here are some Frequently Asked Questions related to Deletion of middle element of linked list are given below.
Ques 1. Can you delete middle element of linked list in constant time?
Ans. No, it is not possible to delete middle element of linked list in constant time because you need to traverse the list to find the middle node.
Ques 2. What is lazy deletion?
Ans. It’s an alternative method to the standard deletion method. Generally, we delete elements logically, but here we delete the elements physically by marking them as deleted by using a boolean value.
Ques 3. What’s the main drawback of a singly linked list?
Ans. As we are aware of the structure of the linked list, the memory which is used is required more as a pointer stores the address of the next element.
Ques 4. What happens if you try to delete a node that is not in the linked list?
Ans. If you try to delete a node that is not in the linked list, the list remains unchanged.


