Last Updated on July 1, 2024 by Abhishek Sharma

Linked lists are a fundamental data structure in computer science, frequently used to store collections of elements. Unlike arrays, linked lists provide dynamic memory allocation and efficient insertions and deletions. Understanding and manipulating linked lists is crucial for solving various computational problems. One common task is determining whether two linked lists are identical. Identical linked lists are those that contain the same sequence of elements in the same order. This article delves into the concept of identical linked lists, explaining their significance, the methodology for comparison, and frequently asked questions related to their identification and usage.
How To Check Two Linked Lists Are Equal
In this problem, we are given two LinkedList and are asked to find if the linked lists are identical or not i.e. we have to find whether the two linked lists have the same arrangement of the values of the nodes in them or not.
Linked list 1:
Linked List 2:

Output: Identical
These two LinkedList are identical.
Let’s first understand the problem statement with the help of an example:
If Linked list 1 = 3→5→7 and Linked list 2 = 3→5→7.
The term ‘arrangement of the values of the nodes in a linked list’ which we have referred to in the problem statement means that if our linked list is 5→6→7→8→9, then the arrangement of the values of the nodes in the linked list is 5,6,7,8,9.
- From the Linked list 1 we can see that its arrangement of the values of the nodes is 3,5,7.
- From the Linked list 2 we can see that its arrangement of the values of the nodes is 3,5,7.
Since both the linked list have the same arrangement of the values of the nodes, so the above linked list 1 and 2 are Identical.
If Linked list 1 = 3→5→6 and Linked list 2 = 3→6→5.
- From the Linked list 1 we can see that its arrangement of the values of the nodes is 3,5,6.
- From the Linked list 2 we can see that its arrangement of the values of the nodes is 3,6,5.
Since both the linked list have a different arrangement of the values of the nodes, so the above linked list 1 and 2 are Not Identical.
Now, I think from the above examples, it is clear what we are trying to find in this problem. So next we will try to think about how we can approach this problem.
Before jumping to the next section of the blog, try to think about how you can solve this problem?
Approach on How To Check Two Linked Lists Are Equal
The basic approach which comes to mind is to traverse both the linked list simultaneously and check if at any iteration:
- The values of the lists are different then we return false.
Else if we reach the end of both the lists at the same time while traversing then only we return true.
Note: If we reach the end in only one list that means their size is different and hence also not identical.
Algorithm on How To Check Two Linked Lists Are Equal
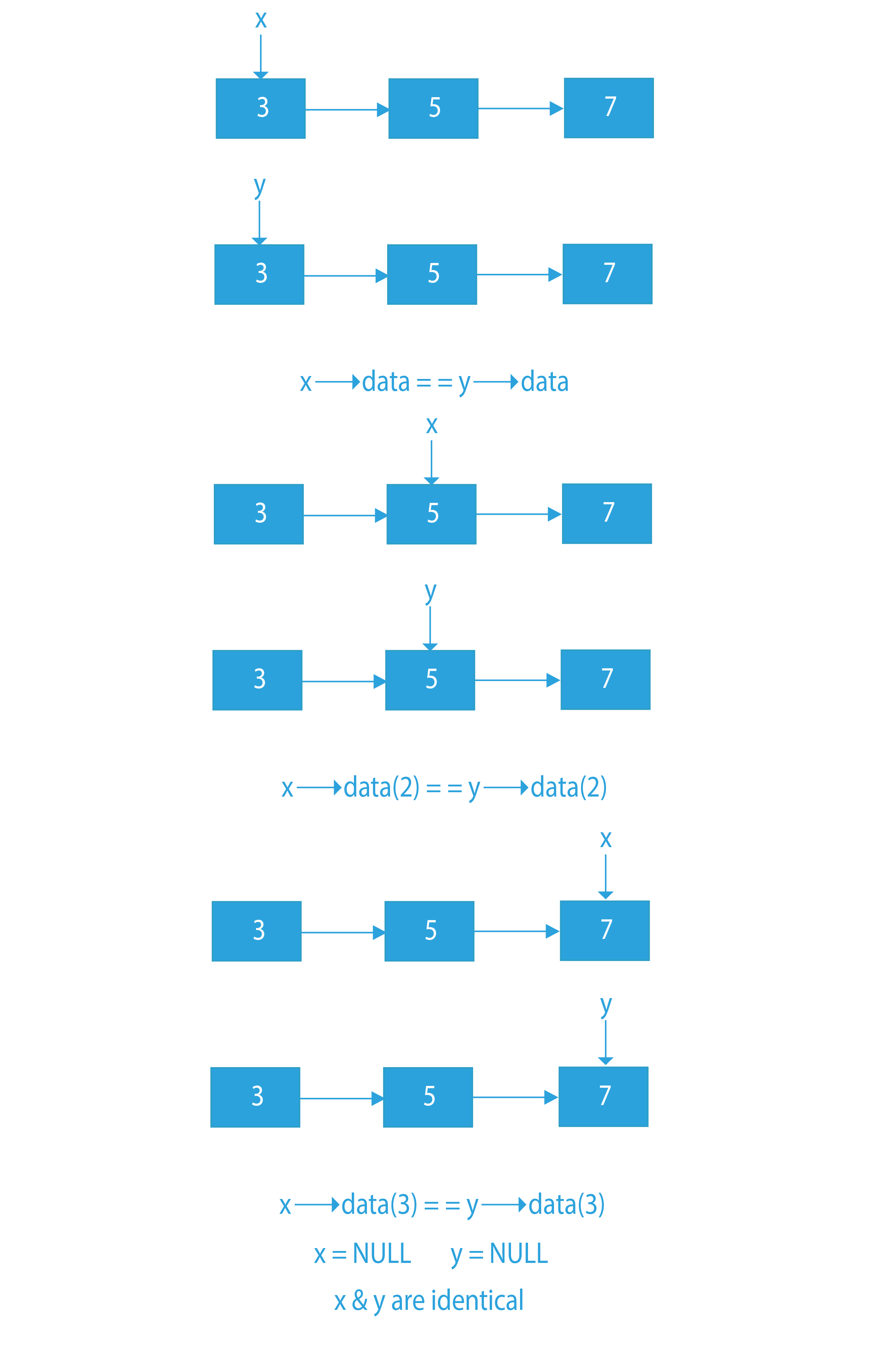
- Start traversing the linked lists x and y.
- If at any point while traversing, the data is different in the two lists (x->data != y->data), then we return false.
- If we reach the end of both the linked list at the same time, then we return true.
- If we reach the end of any one of the lists then they are not identical and return false.
Dry Run on How To Check Two Linked Lists Are Equal
Code Implementation on How To Check Two Linked Lists Are Equal
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
/* Structure for a linked list node */
struct Node
{
int data;
struct Node *next;
};
/* Returns true if linked lists a and b are identical,
otherwise false */
bool areIdentical(struct Node *a, struct Node *b)
{
while (a != NULL && b != NULL)
{
if (a->data != b->data)
return false;
/* If we reach here, then a and b are not NULL and
their data is same, so move to next nodes in both
lists */
a = a->next;
b = b->next;
}
// If linked lists are identical, then 'a' and 'b' must
// be NULL at this point.
return (a == NULL && b == NULL);
}
/* UTILITY FUNCTIONS TO TEST fun1() and fun2() */
/* Given a reference (pointer to pointer) to the head
of a list and an int, push a new node on the front
of the list. */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Driver program to test above function */
int main()
{
/* The constructed linked lists are :
a: 3->2->1
b: 3->2->1 */
struct Node *a = NULL;
struct Node *b = NULL;
push(&a, 1);
push(&a, 2);
push(&a, 3);
push(&b, 1);
push(&b, 2);
push(&b, 3);
areIdentical(a, b)? printf("Identical"):
printf("Not identical");
return 0;
}
#include<bits stdc++.h="">
using namespace std;
struct Node
{
int data;
struct Node *next;
};
bool areIdentical(struct Node *x,struct Node *y)
{
while (x != NULL && y != NULL)
{
if (x->data != y->data)
return false;
x = x->next;
y = y->next;
}
return (x == NULL && y == NULL);
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int main()
{
struct Node *x = NULL;
struct Node *y = NULL;
push(&x, 7);
push(&x, 5);
push(&x, 3);
push(&y, 7);
push(&y, 5);
push(&y, 3);
if(areIdentical(x, y))
cout << "Identical";
else
cout << "Not identical";
return 0;
}
class Identical
{
Node head;
class Node
{
int data;
Node next;
Node(int d) { data = d; next = null; }
}
/* Returns true if linked lists a and b are identical,
otherwise false */
boolean areIdentical(Identical llist2)
{
Node a = this.head, b = llist2.head;
while (a != null && b != null)
{
if (a.data != b.data)
return false;
/* If we reach here, then a and b are not null
and their data is same, so move to next nodes
in both lists */
a = a.next;
b = b.next;
}
// If linked lists are identical, then 'a' and 'b' must
// be null at this point.
return (a == null && b == null);
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
/* Driver program to test above functions */
public static void main(String args[])
{
Identical llist1=new Identical();
Identical llist2=new Identical();
/* The constructed linked lists are :
llist1: 3->2->1
llist2: 3->2->1 */
llist1.push(1);
llist1.push(2);
llist1.push(3);
llist2.push(1);
llist2.push(2);
llist2.push(3);
if (llist1.areIdentical(llist2) == true)
System.out.println("Identical ");
else
System.out.println("Not identical ");
}
}
class Node:
def __init__(self, d):
self.data = d
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def areIdentical(self, listb):
a = self.head
b = listb.head
while (a != None and b != None):
if (a.data != b.data):
return False
a = a.next
b = b.next
return (a == None and b == None)
def push(self, new_data):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node
llist1 = LinkedList()
llist2 = LinkedList()
llist1.push(7)
llist1.push(5)
llist1.push(3)
llist2.push(7)
llist2.push(5)
llist2.push(3)
if (llist1.areIdentical(llist2) == True):
print("Identical ")
else:
print("Not identical ")
Output
IdenticalTime Complexity of Finding identical linked lists: O(min(m,n)), where m,n are the size of the linked lists.
Space Complexity of Finding identical linked lists: O(1), no extra space is used.
Conclusion
Identical linked lists represent a critical concept in understanding and working with linked lists. By ensuring that two linked lists contain the same elements in the same order, we can validate data integrity and perform efficient comparisons. Whether in algorithm design, data processing, or application development, the ability to determine identical linked lists is a valuable skill for any programmer. Through a clear methodology and understanding of common questions, you can effectively identify and utilize identical linked lists in your computational tasks.
FAQ related to Identical Linked Lists
Here are some FAQs related to Identical Linked Lists:
1. What is a linked list?
Answer: A linked list is a data structure consisting of a sequence of elements, each containing a reference (or link) to the next element in the sequence. It allows for efficient insertions and deletions but requires sequential access for element retrieval.
2. How do you define identical linked lists?
Answer: Two linked lists are considered identical if they contain the same number of elements, and each corresponding element in the lists is equal.
3. Why is it important to determine if two linked lists are identical?
Answer: Determining if two linked lists are identical is important for tasks that require data validation, comparison operations, and ensuring data integrity in applications that use linked lists.
4. What is the basic approach to check if two linked lists are identical?
Answer: The basic approach involves traversing both linked lists simultaneously and comparing each corresponding node. If all nodes match and both lists reach their end together, the lists are identical.
5. What are the potential challenges in comparing linked lists for identical elements?
Answer: Challenges include handling different lengths of linked lists, ensuring efficient traversal without excessive time complexity, and managing edge cases such as empty lists or lists with complex data types.
6. Can identical linked lists have different memory addresses for their nodes?
Answer: Yes, identical linked lists can have nodes stored at different memory addresses as long as the data values and their order in the lists are the same.


