Last Updated on November 21, 2022 by Prepbytes

This article taught a famous coding problem of a linked list i.e. Segregate even and odd nodes in a Linked List, this article will help you to grasp hands-on linked list problems. Let’s take a look at the problem statement for a better understanding of Segregate even and odd nodes in a Linked List.
How to Segregate Even and Odd Nodes in a Linked List
In this problem, we are given a Linked List with even and odd valued nodes and are asked to segregate these nodes. Note that we also have to maintain the order in which the nodes were in the original linked list.
Input Linked List:

Output Linked List:
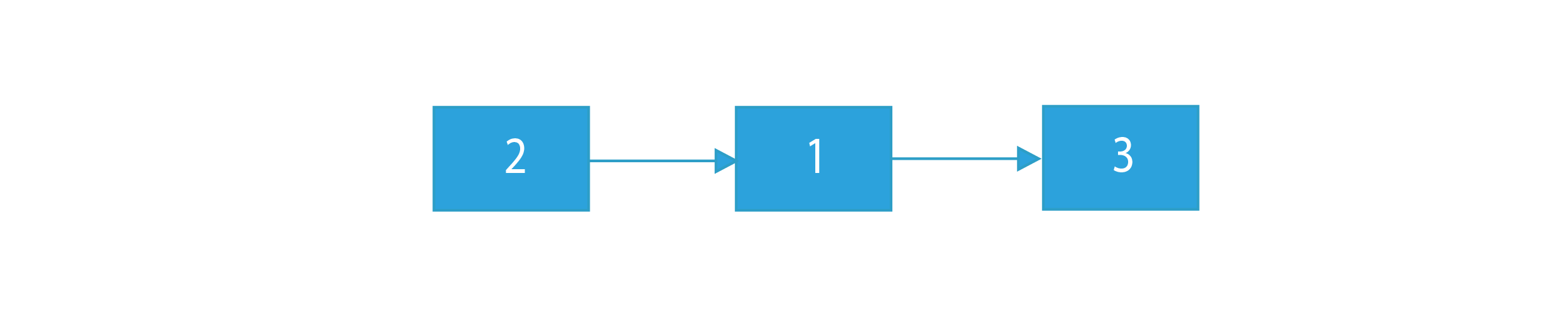
Let’s try to understand the problem with help of an example:
By the way the statement Segregate even and odd nodes indicates that we need to rearrange the nodes of the linked list in such a way that all the even valued nodes appears before odd valued nodes in the modified linked list, and we also have to maintain the order in which the nodes were in the original linked list.
If our linked list is 1→2→3.
Then, while segregating the even and odd nodes of the linked list:
- The node 2 is even valued, so it will come in front, maintaining its order in the original linked list, forming 2.
- The nodes 1 and 3 are odd valued, so will come after 2, maintaining their order in the original linked list, forming 1→3.
Finally, our resultant segregated linked list will be 2→1→3.
If our linked list is 2→1→6→4→8.
Then, while segregating the even and odd nodes of the linked list:
- The nodes 2, 6, 4 and 8 are even valued, so they will come in front, maintaining their order in the original linked list, forming 2→6→4→8.
- The nodes 1 is odd valued, so it will come after 2, 6, 4 and 8 maintaining its order in the original linked list, forming 1.
Finally, our resultant segregated linked list will be 2→6→4→8→1.
Now, I think from the above two examples that it is clear what we have to do in the problems.
Now the main question is how to approach this problem? Try to come up with some approach, not necessarily the optimized one but any approach (if It’s brute force it’s okay, no problem we will optimize it together).
Well, the most naive idea is to create a new Linked List by storing the values of the original Linked List and then inserting the nodes with even value first and then the nodes with odd values, but this will take extra space.
In the above approach we can see that we were able to solve the problem in O(n) time but space complexity is also O(n), so now we need to avoid this extra space.
Note: Generally whenever you get a question on an arrangement in a Linked List avoid dealing with data rather than try to think of a solution using the manipulation of links.
Let’s try to think of some better approach.
Approach of Segregate even and odd nodes in a Linked List
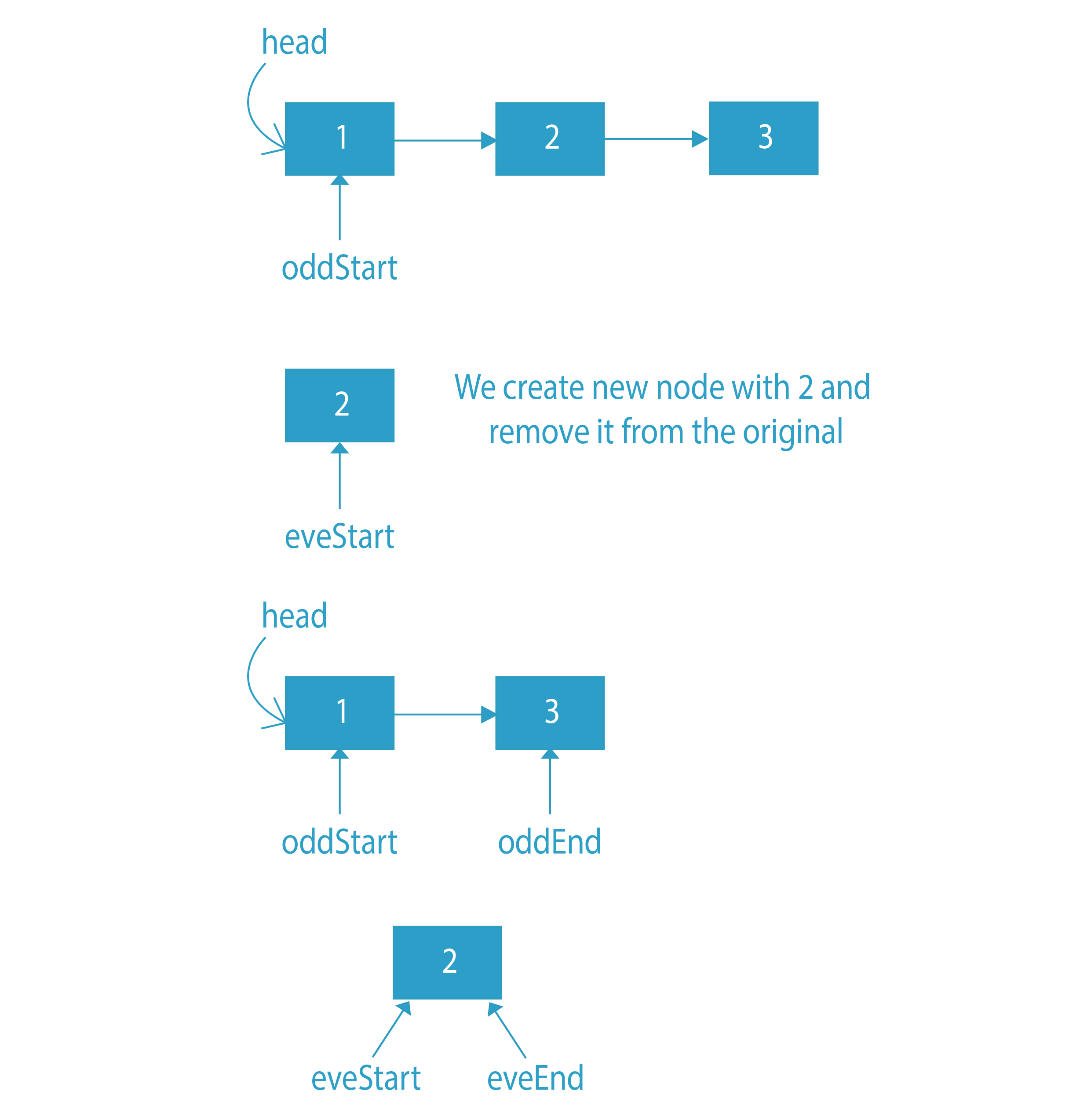
The idea is to split the linked list into two parts containing only even nodes and the other containing only odd nodes. The only task then we will perform is to join these two linked lists together. Let’s see this in algorithm form.
Algorithm of Segregate even and odd nodes in a Linked List
Traverse the linked list:
- For every odd valued node, remove that node from the original linked list and place it in another linked list.
- Continue this till the end of the linked list, and then we will be left with our original linked list containing only the even nodes and another linked list with odd nodes.
- Join these two linked lists and return the head of this linked list.
Dry Run of Segregate even and odd nodes in a Linked List
Code Implementation of Segregate even and odd nodes in a Linked List
#include#include struct Node { int data; struct Node *next; }; void segregateEvenOdd(struct Node **head_ref) { struct Node *evenStart = NULL; struct Node *evenEnd = NULL; struct Node *oddStart = NULL; struct Node *oddEnd = NULL; struct Node *currNode = *head_ref; while(currNode != NULL){ int val = currNode -> data; if(val % 2 == 0) { if(evenStart == NULL){ evenStart = currNode; evenEnd = evenStart; } else{ evenEnd -> next = currNode; evenEnd = evenEnd -> next; } } else{ if(oddStart == NULL){ oddStart = currNode; oddEnd = oddStart; } else{ oddEnd -> next = currNode; oddEnd = oddEnd -> next; } } currNode = currNode -> next; } if(oddStart == NULL || evenStart == NULL){ return; } evenEnd -> next = oddStart; oddEnd -> next = NULL; *head_ref = evenStart; } void push(struct Node** head_ref, int new_data) { struct Node* new_node = (struct Node*)malloc(sizeof(struct Node)); new_node->data = new_data; new_node->next = (*head_ref); (*head_ref) = new_node; } void printList(struct Node *node) { while (node!=NULL) { printf("%d ",node->data); node = node->next; } } int main() { struct Node* head = NULL; push(&head, 3); push(&head, 2); push(&head, 1); segregateEvenOdd(&head); return 0; }
#includestruct Node { int data; struct Node *next; }; void segregateEvenOdd(struct Node **head_ref) { Node *evenStart = NULL; Node *evenEnd = NULL; Node *oddStart = NULL; Node *oddEnd = NULL; Node *currNode = *head_ref; while(currNode != NULL){ int val = currNode -> data; if(val % 2 == 0) { if(evenStart == NULL){ evenStart = currNode; evenEnd = evenStart; } else{ evenEnd -> next = currNode; evenEnd = evenEnd -> next; } } else{ if(oddStart == NULL){ oddStart = currNode; oddEnd = oddStart; } else{ oddEnd -> next = currNode; oddEnd = oddEnd -> next; } } currNode = currNode -> next; } if(oddStart == NULL || evenStart == NULL){ return; } evenEnd -> next = oddStart; oddEnd -> next = NULL; *head_ref = evenStart; } void push(struct Node** head_ref, int new_data) { struct Node* new_node = new Node(); new_node->data = new_data; new_node->next = (*head_ref); (*head_ref) = new_node; } void printList(struct Node *node) { while (node!=NULL) { cout< data; node = node->next; } } int main() { struct Node* head = NULL; push(&head, 3); push(&head, 2); push(&head, 1); segregateEvenOdd(&head); return 0; }
class Seggregate
{
Node head;
class Node
{
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
public void segregateEvenOdd()
{
Node evenStart = null;
Node evenEnd = null;
Node oddStart = null;
Node oddEnd = null;
Node currentNode = head;
while(currentNode != null) {
int element = currentNode.data;
if(element % 2 == 0) {
if(evenStart == null) {
evenStart = currentNode;
evenEnd = evenStart;
} else {
evenEnd.next = currentNode;
evenEnd = evenEnd.next;
}
} else {
if(oddStart == null) {
oddStart = currentNode;
oddEnd = oddStart;
} else {
oddEnd.next = currentNode;
oddEnd = oddEnd.next;
}
}
currentNode = currentNode.next;
}
if(oddStart == null || evenStart == null) {
return;
}
evenEnd.next = oddStart;
oddEnd.next = null;
head=evenStart;
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
void printList()
{
Node temp = head;
while(temp != null)
{
System.out.print(temp.data+" ");
temp = temp.next;
}
System.out.println();
}
public static void main(String args[])
{
Seggregate llist = new Seggregate();
llist.push(3);
llist.push(2);
llist.push(1);
System.out.println("Original Linked List");
llist.printList();
llist.segregateEvenOdd();
System.out.println("Modified Linked List");
llist.printList();
}
}
head = None
class Node:
def __init__(self, data):
self.data = data
self.next =None
def segregateEvenOdd():
global head
end = head
prev = None
curr = head
while (end.next != None):
end = end.next
new_end = end
while (curr.data % 2 !=0 and curr != end):
new_end.next = curr
curr = curr.next
new_end.next.next = None
new_end = new_end.next
if (curr.data % 2 == 0):
head = curr
while (curr != end):
if (curr.data % 2 == 0):
prev = curr
curr = curr.next
else:
prev.next = curr.next
curr.next = None
new_end.next = curr
new_end = curr
curr = prev.next
else:
prev = curr
if (new_end != end and end.data % 2 != 0):
prev.next = end.next
end.next = None
new_end.next = end
def push(new_data):
global head
new_node = Node(new_data)
new_node.next = head
head = new_node
def printList():
global head
temp = head
while(temp != None):
print(temp.data, end = " ")
temp = temp.next
print(" ")
push(3)
push(2)
push(1)
print("Original Linked List")
printList()
segregateEvenOdd()
print("Modified Linked List")
printList()
Output 2 1 3
Time Complexity of Segregate even and odd nodes in a Linked List: O(n), where n is the size of the Linked List.
Space Complexity of Segregate even and odd nodes in a Linked List: O(1), no extra space is used.
Conclusion
This blog tried to explain how to segregate even and odd nodes in a linked list by changing the links of the nodes and not by manipulating the data. As we know, if the nodes contain large data then manipulating data is very expensive and hence changing links is preferred. Also, you can check our practice problem of a linked list that is set by our great mentors, hope these problems will help you to clear linked list doubts. Linked List
FAQs related to Segregate even and odd nodes in a Linked List
1. How do you print odd nodes in a linked list?
To print odd nodes in a linked list:
- Traverse the linked list.
- Maintain a counter pointer to print the odd nodes.
- Check every node whether the counter gives you 0 as the remainder when it is divided by 2, if it does, then print it.
- Increment the counter and move to the next node.
2. Can we reverse a linked list is less than O(N)?
It is not possible to reverse a linked list in less than O(N). A linked list can be reversed only by traversing using an iterative method or recursively.
3. Is the cycle present in a linked list?
There is a cycle present in a linked list if the node reached again while traversing the list.


