Implementation of Deque Using Doubly Linked List

Last Updated on May 26, 2023 by Prepbytes

Implementing a deque (double-ended queue) using a doubly linked list is a common approach in computer programming. A deque is a data structure that allows the insertion and removal of elements from both ends, making it versatile for various applications.

To implement a deque using doubly linked list, we utilize the concept of a doubly linked list, which consists of nodes that contain references to both the previous and next nodes. Each node in the doubly linked list holds an element of the deque.

Deque Implementation using Doubly Linked List

In this problem, we have to implement deque using doubly linked list.

Deque (doubly ended queue) is a linear data structure that stores data in a sequential manner, and It provides the facility to add or remove an element from the front or the back of it in constant time complexity. All the basic functionalities of deque are discussed below.

Functions for Implementing Deque Doubly Linked List

There are various functions that we need for implementation of deque, let us discuss each of them individually.

insertFront(int x): This function adds data at the beginning of the deque.

• For example, let’s say in the deque, the elements are arranged in order – 2,6,3,8.
• If we want to insert an integer ‘7’ in front of the deque, we can do that using the insertFront(7) function.
• After insertion at front the arrangement of elements in deque will become – 7,2,6,3,8.

insertRear(int x): This function adds data at the end of the deque.

• For example, let’s say in the deque, the elements are arranged in order – 2,6,3,8.
• If we want to insert an integer ‘7’ in the end of the deque, we can do that using the insertRear(7) function.
• After insertion at end, the arrangement of elements in deque will become – 2,6,3,8,7

deleteFront(): This function deletes data from the beginning of the deque.

• For example, let’s say in the deque, the elements are arranged in order – 2,6,3,8.
• If we want to delete an element from the front of the deque, we can do that using the deleteFront() function.
• After deletion from the front, the arrangement of elements in deque will become – 6,3,8.

deleteRear(): This function deletes data from the end of the deque.

• For example, let’s say in the deque, the elements are arranged in order – 2,6,3,8.
• If we want to delete an element from the end of the deque, we can do that using the deleteRear() function.
• After deletion from the end, the arrangement of elements in deque will become – 2,6,3

getFront(): This function will return the front element present in the deque.

• For example, let’s say in the deque, the elements are arranged in order – 2,6,3,8.
• So, after calling this function, It will return ‘2’ as it is present at the beginning of the deque.

getRear(): This function will return the last element present in the deque.

• For example, let us say that in our deque, the elements are arranged in order – 2,6,3,8.
• So, after calling this function, It will return ‘8’ as it is present at the end of the deque.

isEmpty(): It returns true if the deque is empty and false when it has at least one element.

size(): It returns the total number of elements present in the deque.

Now that we have seen all the functions we have to build for deque doubly linked list, let’s move to the approach section for deque using doubly linked list.

Also, before directly jumping to the approach section, try to do implementation of deque by yourself. If stuck, no problem, we will thoroughly see in the next section how we can approach this deque doubly linked list.

Approach:

• We need to keep track of the head as well as the tail of our doubly linked list.
• When an element needs to be inserted at the beginning of the linked list, we need to insert it before the head node, update the head, and increase the size of the list by one.
• When an element needs to be inserted at the end of the linked list, we need to insert it after the tail node, update the tail pointer, and decrease the size of the list by one.
• When deleting an element from the beginning, we need to delete the head node and update the head pointer accordingly. Also, after deletion, we have to decrease the size of the list by one.
• When deleting an element from the end, we need to delete the tail node and update the tail pointer accordingly. Also, after deletion, we have to decrease the size of the list by one.

Algorithm to Deque using Doubly Linked List:

1. Initialize two pointers named ‘head’ and ‘tail’ with NULL and variable ‘size’ with zero
2. insertFront for deque doubly linked list function
   a. Create a new node
   b. Check if this node is NULL or not.
   • If it is NULL, it means that memory is full and no further nodes can be created.
   • If it is not NULL, then check if ‘head’ is NULL or not.
     1. If ‘head’ is NULL, that means this is the first node in the list so, assign the address of this newly created node to ‘head’ and ‘tail’
     2. If ‘head’ is not NULL, then
        • Assign the next pointer of the new node to head.
        • Assign the previous pointer of the head to the new node.
        • Update the ‘head’ to the new node’s address
     3. Increment the ‘size’ variable by one.
3. insertRear for deque doubly linked list function
   a. Create a new node.
   b. Check if this node is NULL or not.
   • If it is NULL, it means that memory is full and no further nodes can be created.
   • If it is not NULL, then check if ‘tail’ is NULL or not
     1. If ‘tail’ is NULL, that means this is the first node in the list so, assign the address of this newly created node to ‘head’ and ‘tail’
     2. If ‘tail’ is not NULL then
        • Assign the next pointer of the tail to the new node.
        • Assign the previous pointer of the new node to the tail.
        • Update the ‘tail’ to the new node’s address
     3. Increment the ‘size’ variable by one.
4. deleteFront for deque doubly linked list function
   a. Check if the list is empty or not
   • If the list is empty, return from the function.
   • Else, store the address of ‘head’ in a ‘temp’ variable and advance ‘head’ by one node using head = head→next.
   • If ‘head’ becomes NULL, that means only one node existed in the list, so, make the ‘tail’ NULL as well.
   • Else, make previous of head as NULL.
   • Free the memory from the ‘temp’ node.
   • Decrement the ‘size’ variable by one.
5. deleteRear for deque doubly linked list function
   a. Check if the list is empty or not
   • If the list is empty, return from the function
   • Else, store the address of ‘tail’ in a ‘temp’ variable and advance ‘tail’ by one node using tail = tail→prev.
   • If ‘tail’ becomes NULL, that means only one node existed in the list, so, make the ‘head’ NULL as well.
   • Else, make next of ‘tail’ NULL.
   • Free the memory from the ‘temp’ node.
   • Decrement the ‘size’ variable by one.
6. getFront for deque doubly linked list function
   a. Check if the list is empty or not
   • If it is empty, return from the function saying that the list is empty
   • Else, return the value present in the ‘head’ node
7. getRear function
   a. Check if the list is empty or not
   • If it is empty, return from the function saying that the list is empty
   • Else, return the value present in the ‘tail’ node
8. isEmpty function
   a. If the size is zero, return true.
   b. If the size is not zero, return false.
9. Size for deque doubly linked list:
   a. Return the ‘size’ variable.

Dry Run for Implementation of Deque:

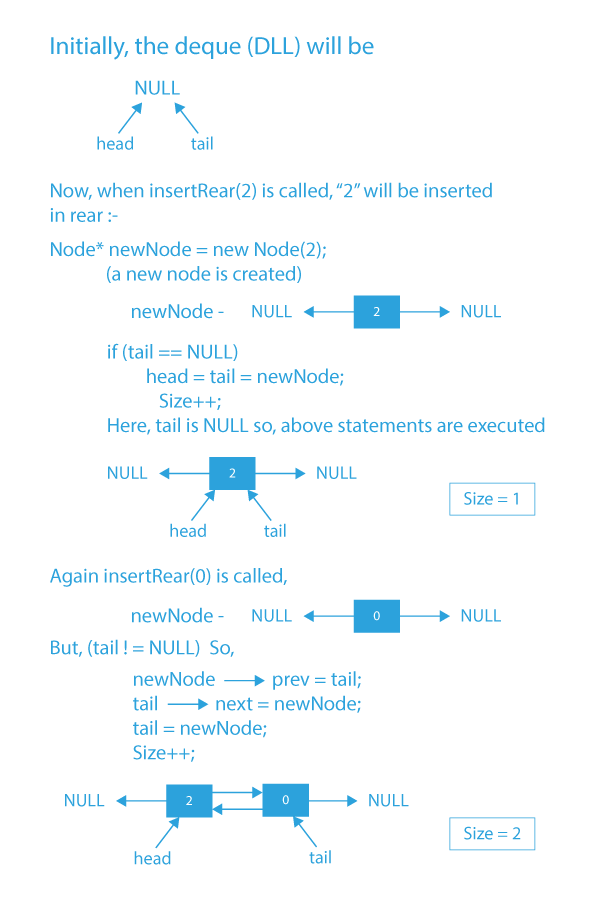
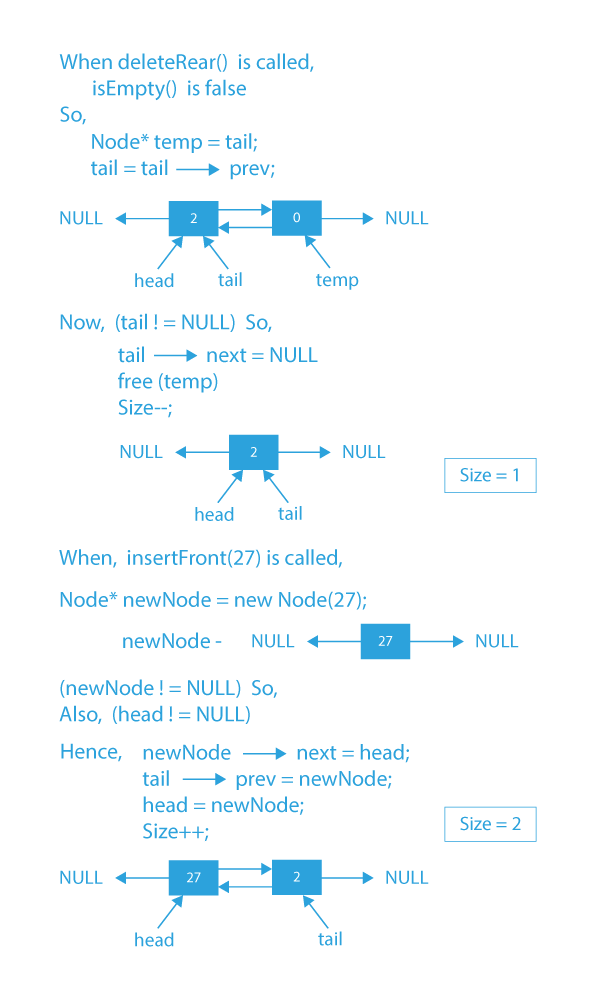
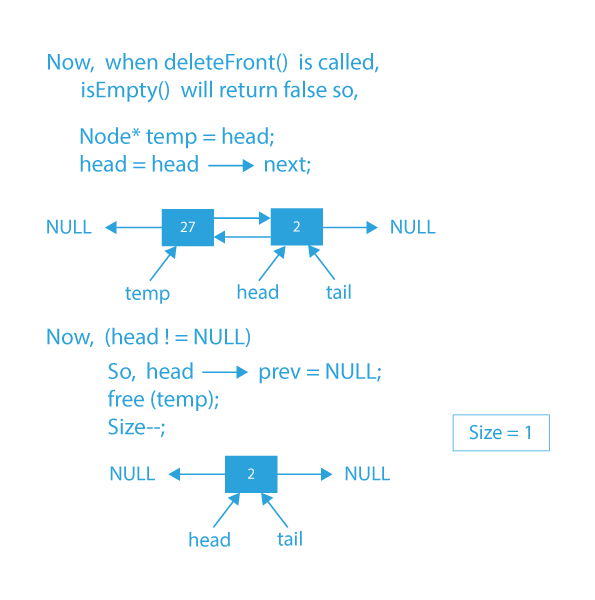
Code Implementation for Deque using Doubly Linked List:

#include 
using namespace std;

// Node structure of a doubly-linked list
class Node
{
    public:
	int data;
	Node *prev, *next;
	// constructor
	Node(int x)
	{
		data = x;
		prev = NULL;
		next = NULL;
	}
};

// A class for deque
class Deque
{
	Node* head;
	Node* tail;
	int Size;

public:
	//initialize deque as stated in step 1 
	Deque()
	{
		head = tail = NULL;
		Size = 0;
	}

	// exhaustive list of functions as discussed above  
	void insertFront(int data);
	void insertRear(int data);
	void deleteFront();
	void deleteRear();
	int getFront();
	int getRear();
	int size();
	bool isEmpty();
};

// this function will check if the deque is empty or not
bool Deque::isEmpty()
{
	return (head == NULL);
}

// This function returns total count of elements in the deque
int Deque::size()
{
	return Size;
}

// This function will insert the element at the front of the    // deque
void Deque::insertFront(int data)
{
	Node* newNode = new Node(data);
	// if newNode is Null then no nodes can be created as 
     // memory is full 
	if (newNode == NULL)
		cout << "OverFlow\n";
	else
	{
		// If deque is empty
		if (head == NULL)
			tail = head = newNode;

		// Inserts an element at the beginning of the list
		else
		{
			newNode->next = head;
			head->prev = newNode;
			head = newNode;
		}

		// Increase size by 1
		Size++;
	}
}

// This function will insert the element at the back of the    // deque
void Deque::insertRear(int data)
{
	Node* newNode = new Node(data);
	// if newNode is Null then no nodes can be created as 
     // memory is full
	if (newNode == NULL)
		cout << "OverFlow\n";
	else
	{
		// If deque is empty
		if (tail == NULL)
			head = tail = newNode;

		// Inserts an element at the end of the list
		else
		{
			newNode->prev = tail;
			tail->next = newNode;
			tail = newNode;
		}
		// Increase size by 1
		Size++;
	}
}

// This function will delete an element from front of the       // deque
void Deque::deleteFront()
{
	// If there are no elements in deque, we cannot delete 
	// anything
	if (isEmpty())
		cout << "UnderFlow\n";

	// Delete the front node and update the ‘head’ pointer as  
     // well as update the links 
	else
	{
		Node* temp = head;
		head = head->next;

		// If only one element was present
		if (head == NULL)
			tail = NULL;
		else
			head->prev = NULL;
		free(temp);

		// Decrease ‘size’ by 1
		Size--;
	}
}

// This function will delete an element from back of the       // deque
void Deque::deleteRear()
{
	// If there are no elements in deque, we cannot delete 
	// anything
	if (isEmpty())
		cout << "UnderFlow\n";

	// Delete the back node and update the ‘tail’ pointer as  
     // well as update the links
	else
	{
		Node* temp = tail;
		tail = tail->prev;

		// If only one element was present
		if (tail == NULL)
			head = NULL;
		else
			tail->next = NULL;
		free(temp);

		// Decrease ‘size’ by 1
		Size--;
	}
}

// this function will return front element of the deque
int Deque::getFront()
{
	// If there are no elements in deque, return -1
	if (isEmpty())
		return -1;
	return head->data;
}

// this function will return rear element of the deque
int Deque::getRear()
{
	// If there are no elements in deque, return -1
	if (isEmpty())
		return -1;
	return tail->data;
}


int main()
{
	Deque dq;
	cout << "Insert element '2' at rear end\n";
	dq.insertRear(2);

	cout << "Insert element '0' at rear end\n";
	dq.insertRear(0);

	cout << "Rear end element: "
		<< dq.getRear() << endl;

	dq.deleteRear();
	cout << "After deleting rear element new rear"
		<< " is: " << dq.getRear() << endl;

	cout << "Inserting element '27' at front end \n";
	dq.insertFront(27);

	cout << "Front end element: "
		<< dq.getFront() << endl;

	cout << "Number of elements in Deque: "
		<< dq.size() << endl;

	dq.deleteFront();
	cout << "After deleting front element new "
		<< "front is: " << dq.getFront() << endl;

	return 0;
}

Output of deque using doubly linked list –

Insert element ‘2’ at rear end
Insert element ‘0’ at rear end
Rear end element: 0
After deleting rear element new rear is: 2
Inserting element ’27’ at front end
Front end element: 27
Number of elements in Deque: 2
After deleting front element new front is: 2

Time complexity: For all operations except erase(), the time complexity is O(1). For erase() time complexity is O(n).

**Conclusion**
In conclusion, implementing a deque (double-ended queue) using a doubly linked list provides an efficient and versatile data structure that supports insertion and removal of elements from both ends. The use of a doubly linked list allows for easy traversal in both directions, making the implementation straightforward and efficient.

By utilizing the push_front, push_back, pop_front, and pop_back operations, we can add and remove elements from the front and back of the deque in constant time. Additionally, accessing the front and back elements is also efficient with constant time complexity.

The implementation of a deque using a doubly linked list is beneficial in scenarios where fast insertion and removal of elements at both ends are required. It offers flexibility in managing collections of data and can be used in various applications, such as queueing systems, simulations, and data processing tasks.

FAQs related to Deque

1. Is Deque a doubly linked list?

We can say that by using a doubly linked list we can implement a deque and we can also call it a head-tail linked list.

2. How is a doubly linked list different from a deque?

Basically, a dequeue only allows insertion (and deletion) at the front and back, while a list allows insertion in the middle of it.

3. In which data structure insertion or deletion of an element can be done in constant time?

Doubly linked list