In this blog, we will see an interesting question i.e. how to merge two linked list alternatively let us look at what the problem says.
How to Merge Two Linked List Alternatively
In this problem, we are given two linked lists, A and B. We should merge the second list into the first one at alternate positions. The second linked list should become empty.
Let’s try to understand this problem with help of examples.
Suppose the given linked lists are:
We have add the elements of the second list to the first list, at alternate positions.
-
First, we will add the first element of B after the first element of A –
-
Now, add the second element of B after the second element of old A –
-
Now, add the third element of B after the third element of old A
-
Now, add the fourth element of B after the fourth element of old A
B: Empty list
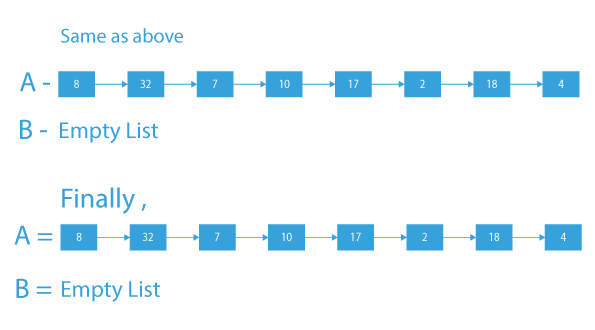
After adding the elements of the second list to the first list at alternate positions, the final list will be:
Input:
Output:
Explanation:The nodes of the second linked list are merged with the first linked list at alternate positions.
I think from the above example the problem statement is clear, so we should now think how we can approach this problem. Try to come up with a approach, it may be bruteforce but before jumping to approach section try to think how will you approach it.
Note: We should keep in mind that we cannot create a new linked list. We have to alter the first list.
Approach of merge two linked list alternatively
The main idea is to iterate using a loop while there are available positions in the first list and insert nodes of the linked list by changing pointers. We should also note that the head of the first link will never change, but the head of the second list may change, so we have to use one pointer for the first list and two pointers for the second list. We can get a better idea by looking at the algorithm.
Algorithm of merge two linked list alternatively
- Traverse in FirstList until there are available positions in it.
- Loop in SecondList and insert nodes of SecondList to FirstList.
- Do insertion by changing pointers.
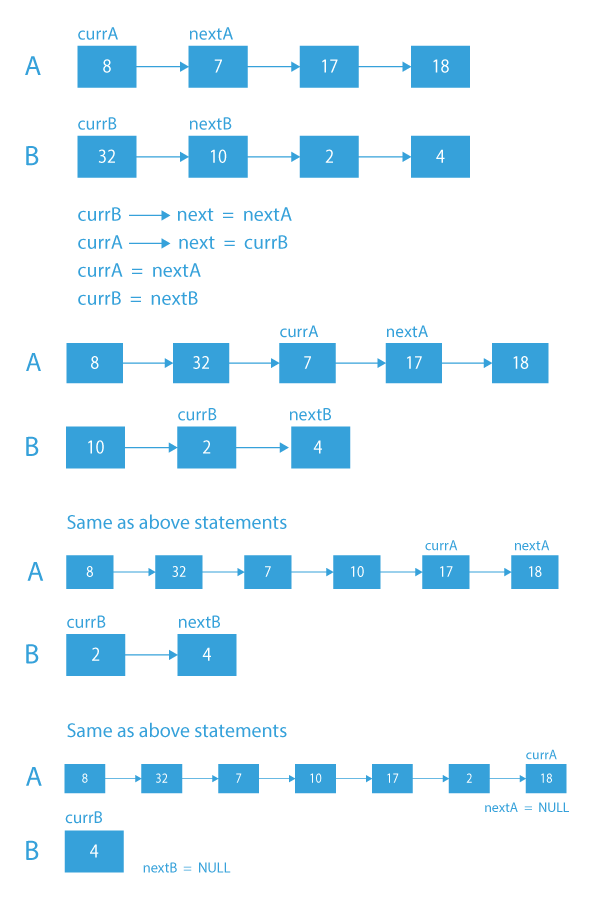
- Store next pointers of both A and B in nextA and nextB and current pointers of both A and B in currA and currB.
- Make B as the next of pointer A and next of pointer B is next of pointer A. By doing this we insert a node of SecondList in FirstList:
currB – > next = nextA
currA – > next = currB
currA=nextA
currB=nextB - Move pointers of FirstList and SecondList and again perform the above steps of insertion of list B nodes in list A at alternate position.
Dry Run of merge two linked list alternatively
Code Implementation of merge two linked list alternatively
#include <stdio.h>
#include <stdlib.h>
// A nexted list node
struct Node
{
int data;
struct Node *next;
};
/* Function to insert a node at the beginning */
void push(struct Node ** head_ref, int new_data)
{
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
/* Utility function to print a singly linked list */
void printList(struct Node *head)
{
struct Node *temp = head;
while (temp != NULL)
{
printf("%d ", temp->data);
temp = temp->next;
}
printf("\n");
}
// Main function that inserts nodes of linked list q into p at
// alternate positions. Since head of first list never changes
// and head of second list may change, we need single pointer
// for first list and double pointer for second list.
void merge(struct Node *p, struct Node **q)
{
struct Node *p_curr = p, *q_curr = *q;
struct Node *p_next, *q_next;
// While there are available positions in p
while (p_curr != NULL && q_curr != NULL)
{
// Save next pointers
p_next = p_curr->next;
q_next = q_curr->next;
// Make q_curr as next of p_curr
q_curr->next = p_next; // Change next pointer of q_curr
p_curr->next = q_curr; // Change next pointer of p_curr
// Update current pointers for next iteration
p_curr = p_next;
q_curr = q_next;
}
*q = q_curr; // Update head pointer of second list
}
// Driver program to test above functions
int main()
{
struct Node *p = NULL, *q = NULL;
push(&p, 3);
push(&p, 2);
push(&p, 1);
printf("First Linked List:\n");
printList(p);
push(&q, 8);
push(&q, 7);
push(&q, 6);
push(&q, 5);
push(&q, 4);
printf("Second Linked List:\n");
printList(q);
merge(p, &q);
printf("Modified First Linked List:\n");
printList(p);
printf("Modified Second Linked List:\n");
printList(q);
getchar();
return 0;
}
#include <bits stdc++.h="">
using namespace std;
struct LLNode
{
int data;
struct LLNode* next;
};
void insertAtBeginning(struct LLNode** head, int dataToBeInserted)
{
struct LLNode* curr = new LLNode;
curr->data = dataToBeInserted;
curr->next = NULL;
if(*head == NULL)
*head=curr;
else
{
curr->next=*head;
*head=curr;
}
}
void display(struct LLNode**node)
{
struct LLNode *temp= *node;
if (temp==NULL)
{
cout<<"Empty linked list"<<endl; }="" while(temp!="NULL)" {="" if(temp-="">next!=NULL)
cout<<temp->data<<" ->";
else
cout<<temp->data;
temp=temp->next;
}
cout<<endl; }="" void="" merge(struct="" llnode="" *a,="" struct="" **b)="" {="" *curra="A," *currb="*B;" *nexta,="" *nextb;="" while="" (curra="" !="NULL" &&="" currb="" nexta="currA-">next;
nextB = currB->next;
currB->next = nextA;
currA->next = currB;
currA = nextA;
currB = nextB;
}
*B = currB;
}
int main()
{
struct LLNode *FirstList = NULL, *SecondList = NULL;
insertAtBeginning(&FirstList, 18);
insertAtBeginning(&FirstList, 17);
insertAtBeginning(&FirstList, 7);
insertAtBeginning(&FirstList, 8);
insertAtBeginning(&SecondList, 4);
insertAtBeginning(&SecondList, 2);
insertAtBeginning(&SecondList, 10);
insertAtBeginning(&SecondList, 32);
cout<<"Linked List A: ";
display(&FirstList);
cout<<"Linked List B: ";
display(&SecondList);
cout<<"Merging List B into List A at alternate positions in A";
Merge(FirstList,&SecondList);
cout<<"\nOutput Linked List A: ";
display(&FirstList);
cout<<"Output Linked List B: ";
display(&SecondList);
return 0;
}
public class LinkedList
{
Node head;
class Node
{
int data;
Node next;
Node(int d) {data = d; next = null; }
}
void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
void merge(LinkedList q)
{
Node p_curr = head, q_curr = q.head;
Node p_next, q_next;
while (p_curr != null && q_curr != null) {
p_next = p_curr.next;
q_next = q_curr.next;
q_curr.next = p_next;
p_curr.next = q_curr;
p_curr = p_next;
q_curr = q_next;
}
q.head = q_curr;
}
void printList()
{
Node temp = head;
while (temp != null)
{
System.out.print(temp.data+" ");
temp = temp.next;
}
System.out.println();
}
public static void main(String args[])
{
LinkedList llist1 = new LinkedList();
LinkedList llist2 = new LinkedList();
llist1.push(18);
llist1.push(17);
llist1.push(7);
llist1.push(8);
System.out.println("Linked List A: ");
llist1.printList();
llist2.push(4);
llist2.push(2);
llist2.push(10);
llist2.push(32);
System.out.println("Linked List B: ");
System.out.println("Merging List B into List A at alternate positions in A");
llist1.merge(llist2);
System.out.println("Output Linked List A: ");
llist1.printList();
System.out.println("Output Linked List B: ");
llist2.printList();
}
}
class Node(object):
def __init__(self, data:int):
self.data = data
self.next = None
class LinkedList(object):
def __init__(self):
self.head = None
def push(self, new_data:int):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node
def printList(self):
temp = self.head
while temp != None:
print(temp.data,end=" ")
temp = temp.next
def merge(self, p, q):
p_curr = p.head
q_curr = q.head
while p_curr != None and q_curr != None:
p_next = p_curr.next
q_next = q_curr.next
q_curr.next = p_next
p_curr.next = q_curr
p_curr = p_next
q_curr = q_next
q.head = q_curr
llist1 = LinkedList()
llist2 = LinkedList()
llist1.push(18)
llist1.push(17)
llist1.push(7)
llist1.push(8)
llist2.push(4)
llist2.push(2)
llist2.push(10)
llist2.push(32)
print("First Linked List:")
llist1.printList()
print("\nSecond Linked List:")
llist2.printList()
llist1.merge(p=llist1, q=llist2)
print("\nModified first linked list:")
llist1.printList()
print("\nModified second linked list:")
llist2.printList()
Output
Linked List A: 5 ->7 ->17 ->13
Linked List B: 12 ->10 ->2 ->4
Merging List B into List A at alternate positions in A
Output Linked List A: 5 ->12 ->7 ->10 ->17 ->2 ->13 ->4
Output Linked List B: Empty linked list
Space Complexity merge two linked list alternatively: O(1), as only temporary variables are being created.
Conclusion
To summarize the talk, we looked at the problem approach, and merge two linked list alternatively. Since the problem was related to a linked list, don’t stop here, just check the questions created by our mentors over the linked list. Linked List.
FAQs related to merge two linked list alternatively
1. In which area of the memory, a linked list is saved?
Linked lists are created using dynamic memory allocation, say malloc. The heap is used for dynamic memory allocations. The heap is a global resource that contains all of the system’s free memory. The heap is treated as a linked list of unused memory blocks, known as the free list.
2. How much memory does a linked list use?
Linked List only utilizes the nodes it needs, which can be as small as 24 bytes.
3. What are the real-time applications of linked lists?
Image viewer – Since the previous and next images are linked, they can be accessed using the next and previous buttons.
Previous and next page in a web browser – Since they are linked as a linked list, we may access the previous and next URL searched in a web browser by hitting the back and next buttons.
Music Player – The previous and next songs in the music player are linked. You can play songs from the beginning or finish of the list.