Merge Sort on a Singly Linked List

Last Updated on November 4, 2022 by Prepbytes

Introduction

Sorting is the process of arranging the elements that can be placed either in ascending or descending order. There are different sorting algorithms that can be used for arranging data in a lighting-fast manner having different time complexities In this article, we will learn how to merge sort for linked list .

Problem Statement for merge sort in linked list

According to the problem statement, we are given a singly linked list, and we need to sort this singly linked list using merge sort.

Merge Sort

Merge sort is a divide and conquer algorithm.

• It is a recursive algorithm.
• In merge sort, we have to divide the container (container can be an array, list etc.) into two halves, and then we will call merge sort recursively on the two halves.
• These two merge sort call return a sorted container, and we then merge this sorted container so that the whole container remains sorted.
• Have a look at the below image to see in a nutshell how merge sort works.

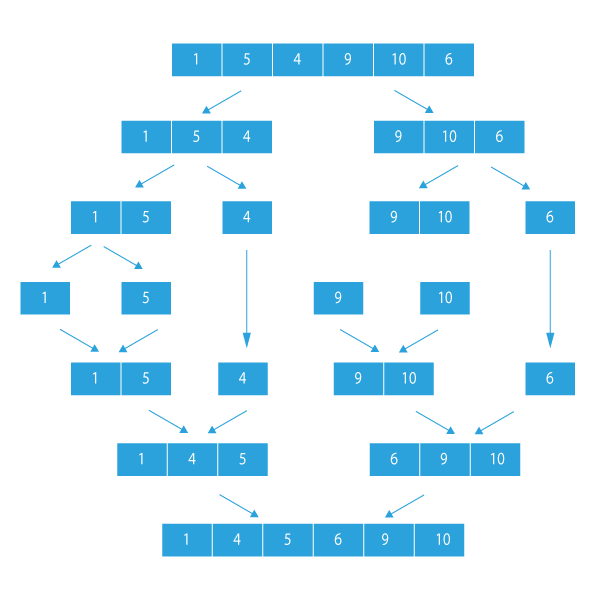
Now, we have a brief understanding of the merge sort algorithm. Let’s learn how to apply merge sort for linked list.

In the case for applying merge sort in linked list, we will recursively divide the list into two sub-lists at each step till list size is reduced to one and while backtracking from the recursive call, we have two sorted lists, which will be merged together into a single list by merge operation in linear time.

Now we will look at the approach and algorithm for applying merge sort in linked list.

Approach and Algorithm for merge sort for linked list (Merge Sort)

1. If the head of the linked list is NULL or (head→ next == NULL), it shows that our linked list is of size 1 or 0 and a linked list of size zero or one is already sorted. So, Don’t do anything, just return head.
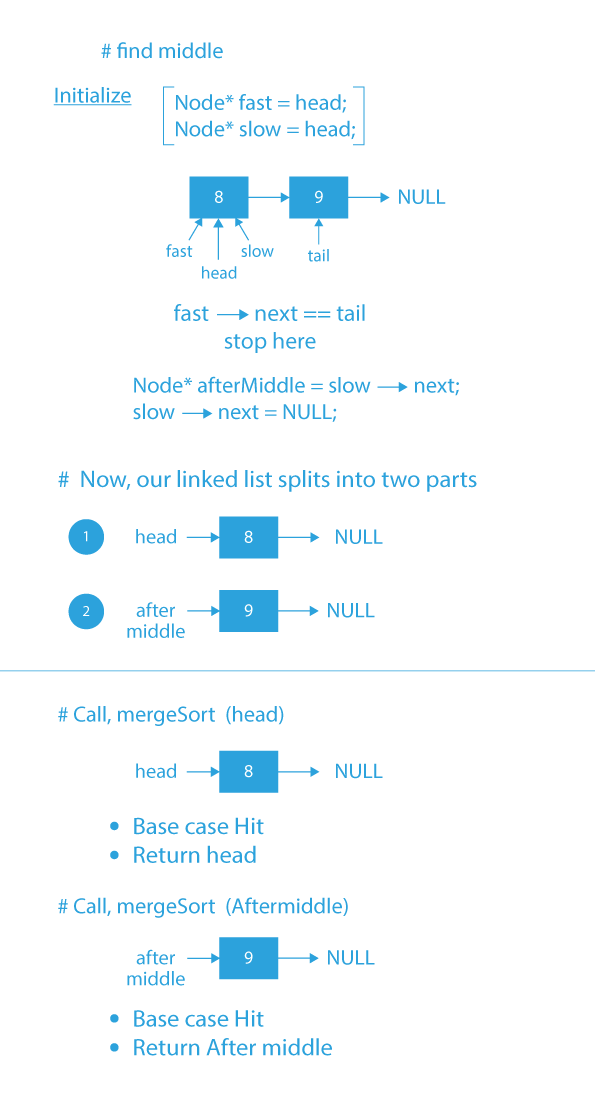
2. If the linked list is of size > 1 then first find the middle of the linked list.
• For finding middle node, use slow and fast pointer method.
• In this method, we take two pointers slow and fast and initialize them with head.
• Then we move the slow pointer by one node and fast pointer by 2 nodes until the fast pointer reaches the tail of the list.
• And when the fast pointer reaches the tail, the slow pointer will be at the middle of the linked list.
• The only reason why slow pointer will be at the middle of the list, when fast reaches tail is because the slow pointer is moving with half the speed of fast pointer and when the fast pointer has traversed the complete list till then the slow pointer will have only traversed half the list, so that’s why slow pointer will be at the middle of the list.
3. Now, store slow → next in a pointer named afterMiddle and assign slow → next = NULL.
4. Recursively call mergeSort() on both left and right sub-linked list and store the new head of the left and right linked list in pointer variable part1 and part2.
5. When the recursive call on the left and right sub-list returns, merge the two linked lists returned by recursive calls (remember that the recursive call will return the sorted lists).
6. Return the final head of the merged linked list.

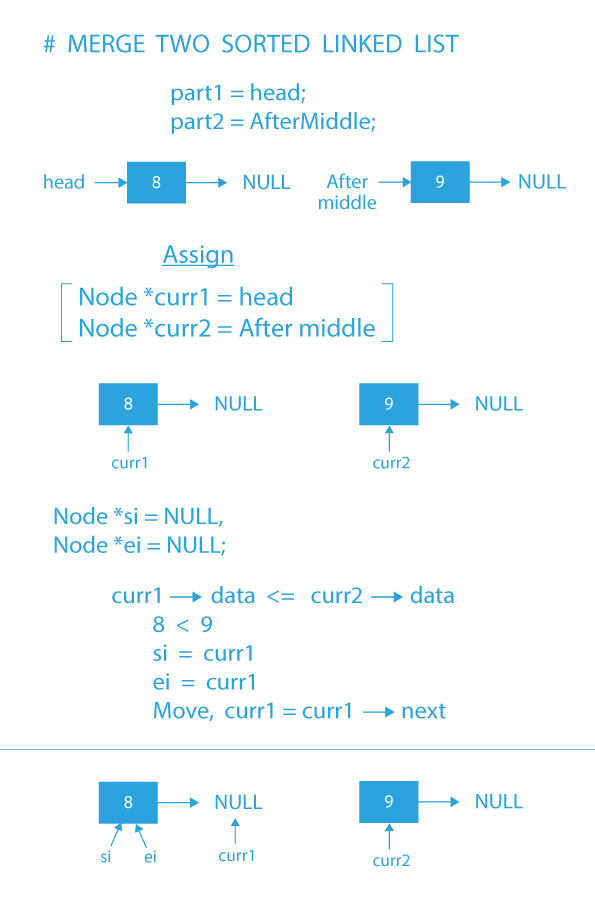
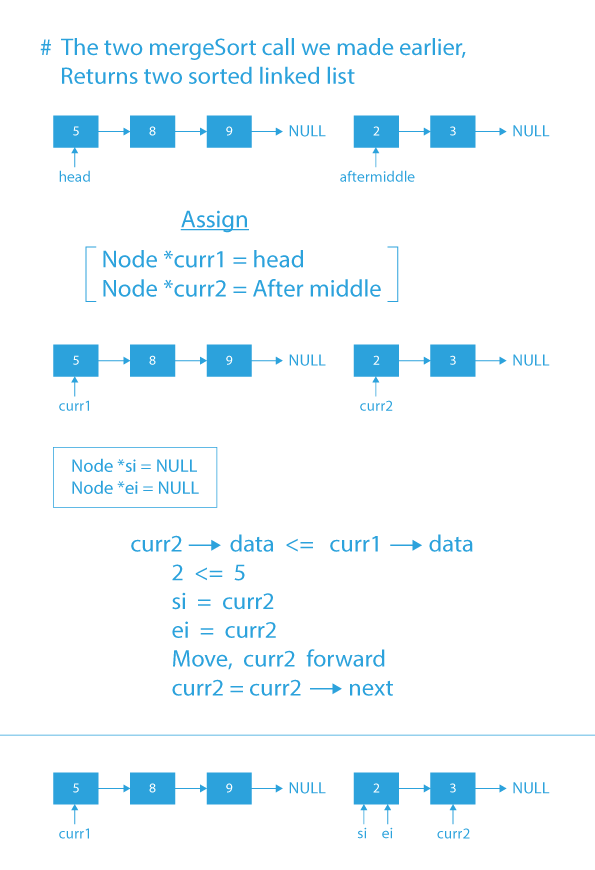
Merging two sorted linked list Algorithm:

When the two recursive calls will return the two sorted lists, then we will merge that sorted list into a single list using these below steps.

1. Initialize two pointer variables named curr1 and curr2 with left sorted sub-list and right sorted sub-list.
2. Initialize two pointer variable named si and ei with NULL; these two pointer variables are the head and tail of the final sorted linked list.
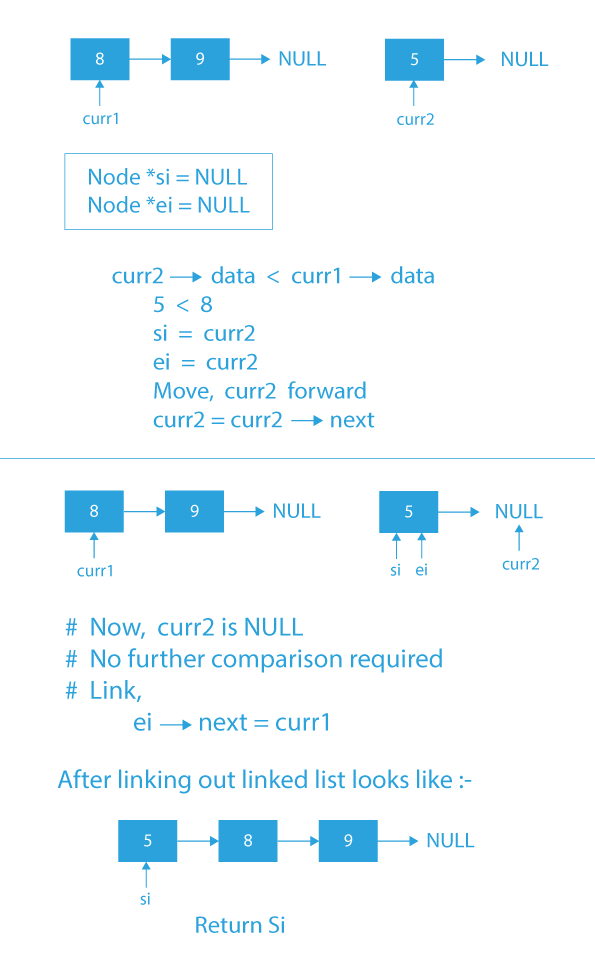
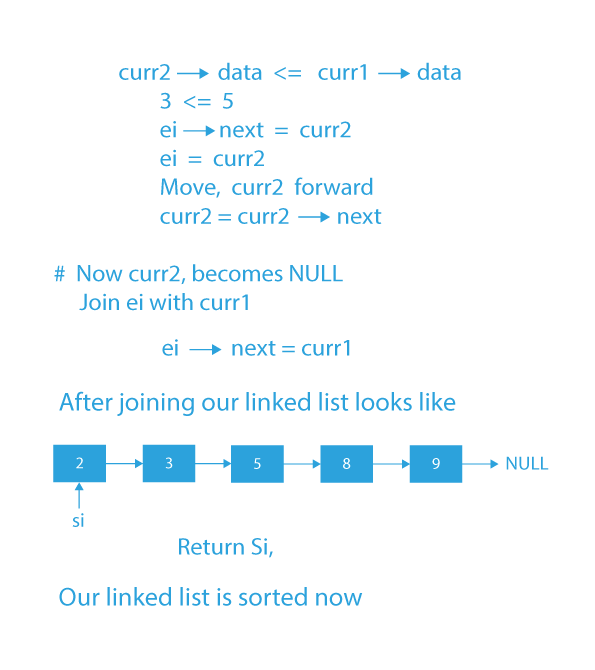
3. If the data of curr1 is less than the data of curr2, then, store curr1 in next of ei & move curr1 to the next of curr1.
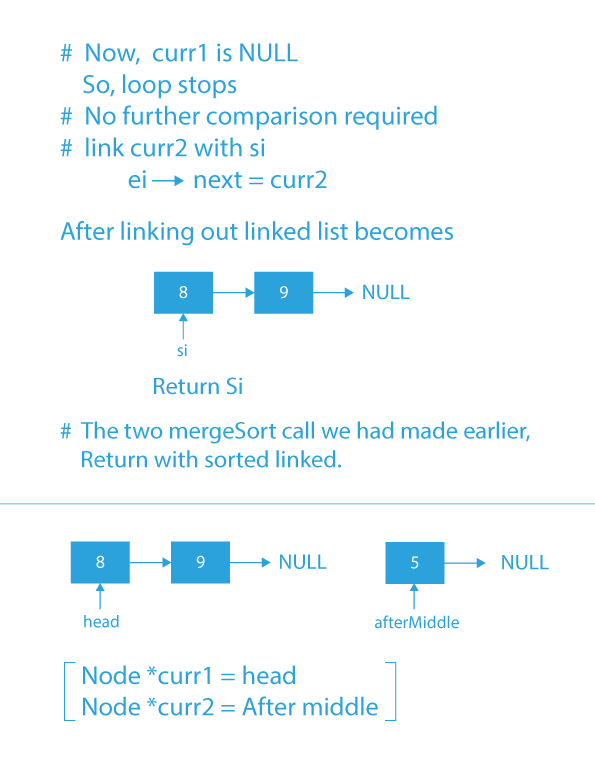
4. Else, if the data of curr2 is less than the data of curr1, then store curr2 in next of ei & move curr2 to the next of curr2.
5. Repeat steps 3 and 4 until either of the curr1 or curr2 is not equal to NULL.
6. Now add any remaining nodes of the first or the second linked list to the merged linked list.
7. Return the head of the merged sorted linked list containing all the nodes of the two sorted sub-lists.

Dry Run

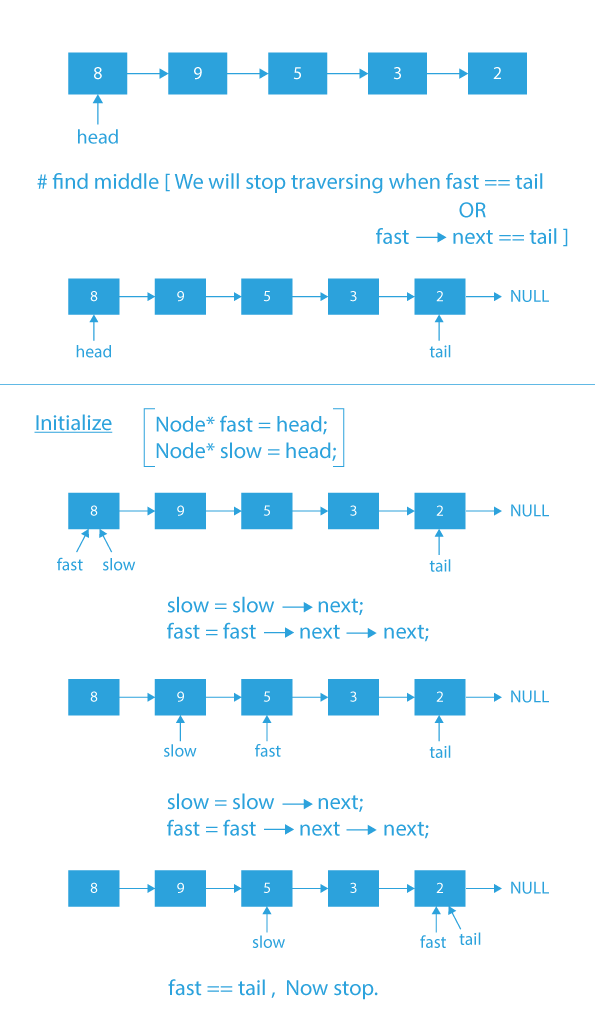
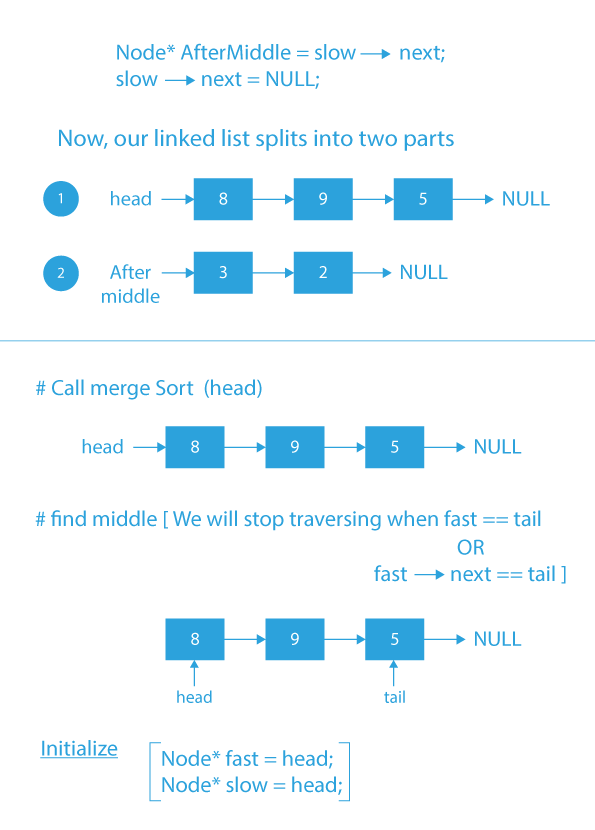
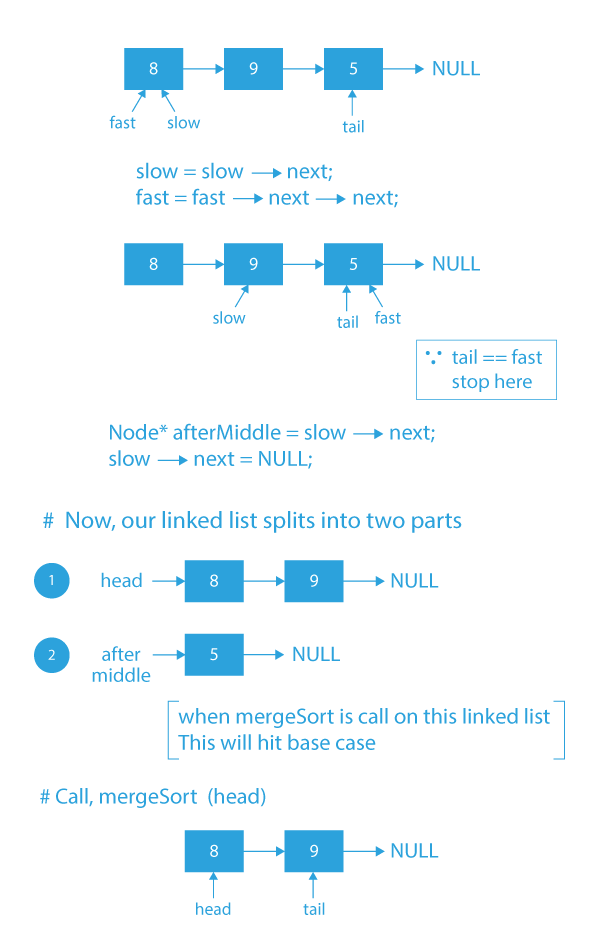
Code Implementation

#include 
#include 
 
/* Link list node */
struct Node {
    int data;
    struct Node* next;
};
 
/* function prototypes */
struct Node* SortedMerge(struct Node* a, struct Node* b);
void FrontBackSplit(struct Node* source,
                    struct Node** frontRef, struct Node** backRef);
 
/* sorts the linked list by changing next pointers (not data) */
void MergeSort(struct Node** headRef)
{
    struct Node* head = *headRef;
    struct Node* a;
    struct Node* b;
 
    /* Base case -- length 0 or 1 */
    if ((head == NULL) || (head->next == NULL)) {
        return;
    }
 
    /* Split head into 'a' and 'b' sublists */
    FrontBackSplit(head, &a, &b);
 
    /* Recursively sort the sublists */
    MergeSort(&a);
    MergeSort(&b);
 
    /* answer = merge the two sorted lists together */
    *headRef = SortedMerge(a, b);
}
 
/* See https:// www.geeksforgeeks.org/?p=3622 for details of this
function */
struct Node* SortedMerge(struct Node* a, struct Node* b)
{
    struct Node* result = NULL;
 
    /* Base cases */
    if (a == NULL)
        return (b);
    else if (b == NULL)
        return (a);
 
    /* Pick either a or b, and recur */
    if (a->data <= b->data) {
        result = a;
        result->next = SortedMerge(a->next, b);
    }
    else {
        result = b;
        result->next = SortedMerge(a, b->next);
    }
    return (result);
}
 
/* UTILITY FUNCTIONS */
/* Split the nodes of the given list into front and back halves,
    and return the two lists using the reference parameters.
    If the length is odd, the extra node should go in the front list.
    Uses the fast/slow pointer strategy. */
void FrontBackSplit(struct Node* source,
                    struct Node** frontRef, struct Node** backRef)
{
    struct Node* fast;
    struct Node* slow;
    slow = source;
    fast = source->next;
 
    /* Advance 'fast' two nodes, and advance 'slow' one node */
    while (fast != NULL) {
        fast = fast->next;
        if (fast != NULL) {
            slow = slow->next;
            fast = fast->next;
        }
    }
 
    /* 'slow' is before the midpoint in the list, so split it in two
    at that point. */
    *frontRef = source;
    *backRef = slow->next;
    slow->next = NULL;
}
 
/* Function to print nodes in a given linked list */
void printList(struct Node* node)
{
    while (node != NULL) {
        printf("%d ", node->data);
        node = node->next;
    }
}
 
/* Function to insert a node at the beginning of the linked list */
void push(struct Node** head_ref, int new_data)
{
    /* allocate node */
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
 
    /* put in the data */
    new_node->data = new_data;
 
    /* link the old list off the new node */
    new_node->next = (*head_ref);
 
    /* move the head to point to the new node */
    (*head_ref) = new_node;
}
 
/* Driver program to test above functions*/
int main()
{
    /* Start with the empty list */
    struct Node* res = NULL;
    struct Node* a = NULL;
 
    /* Let us create a unsorted linked lists to test the functions
Created lists shall be a: 2->3->20->5->10->15 */
    push(&a, 15);
    push(&a, 10);
    push(&a, 5);
    push(&a, 20);
    push(&a, 3);
    push(&a, 2);
 
    /* Sort the above created Linked List */
    MergeSort(&a);
 
    printf("Sorted Linked List is: \n");
    printList(a);
 
    getchar();
    return 0;
}

#include
using namespace std;

/* structure of node */
class Node{
public:
    int data;
    Node* next;
    Node(int data){
        this->data = data;
        this->next = NULL;
    }
};


/* print linked list */
void printList(Node* node){
    while (node != NULL) {
        cout<data<<" ";
        node = node->next;
    }
    printf("\n");
}

/* find and return middle node of the linked list*/
Node* middle(Node* head, Node* tail) {
        Node* slow = head;
        Node* fast = head;
        
        while(fast!=tail && fast->next!=tail){
            slow = slow->next;
            fast = fast->next->next;
        }
        Node* afterMiddle = slow->next;
        slow->next = NULL;
        return afterMiddle;
}
/* merge sort*/
Node* mergeSort(Node* head){
    if(head == NULL || head->next == NULL){
        return head;
    }

    Node* tail = head;

    while(tail->next){
        tail = tail->next;
    }


    Node* afterMiddle = middle(head, tail);
    Node* part1 = mergeSort(head);
    Node* part2 = mergeSort(afterMiddle);

    Node *curr1 = part1, *curr2 = part2;


    Node *si = NULL, *ei = NULL;

    while(curr1 && curr2){
        if(curr1->data <= curr2->data){
            if(si == NULL){
                si = curr1;
                ei = curr1;
            }else{
                ei->next = curr1;
                ei = curr1;
            }
            curr1 = curr1->next;
        }else{
            if(si == NULL){
                si = curr2;
                ei = curr2;
            }else{
                ei->next = curr2;
                ei = curr2;
            }
            curr2 = curr2->next;
        }
    }


    while(curr1){
        ei->next = curr1;
        ei = curr1;
        curr1 = curr1->next;
    }

    while(curr2){
        ei->next = curr2;
        ei = curr2;
        curr2 = curr2->next;
    }


    return si;
}



int main(){
    Node n1 = Node(8);
    Node n2 = Node(9);
    Node n3 = Node(5);
    Node n4 = Node(3);
    Node n5 = Node(2);
    Node n6 = Node(7);
    n1.next = &n2;
    n2.next = &n3;
    n3.next = &n4;
    n4.next = &n5;
    n5.next = &n6;

    Node* head = &n1;
    cout << "Linked List before sorting \n";
    printList(head);
 
    head = mergeSort(head);
 
    cout << "Linked List after sorting \n";
    printList(head);
}

class Node 
{
    int data;
    Node next;
    Node(int key)
    {
        this.data = key;
        next = null;
    }
}
class MergeSort 
{
    // Function to merge sort
    static Node mergeSort(Node head)
    {
        if (head.next == null)
            return head;

        Node mid = findMid(head);
        Node head2 = mid.next;
        mid.next = null;
        Node newHead1 = mergeSort(head);
        Node newHead2 = mergeSort(head2);
        Node finalHead = merge(newHead1, newHead2);

        return finalHead;
    }
    // Function to merge two linked lists
    static Node merge(Node head1, Node head2)
    {
        Node merged = new Node(-1);
        Node temp = merged;
    
        // While head1 is not null and head2 is not null
        while (head1 != null && head2 != null) {
            if (head1.data < head2.data) {
                temp.next = head1;
                head1 = head1.next;
            }
            else {
                temp.next = head2;
                head2 = head2.next;
            }
            temp = temp.next;
        }
        // While head1 is not null
        while (head1 != null) {
            temp.next = head1;
            head1 = head1.next;
            temp = temp.next;
        }
        // While head2 is not null
        while (head2 != null) {
            temp.next = head2;
            head2 = head2.next;
            temp = temp.next;
        }
        return merged.next;
    }
    // Find mid using The Tortoise and The Hare approach
    static Node findMid(Node head)
    {
        Node slow = head, fast = head.next;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
    static void printList(Node head)
    {
        while (head != null) {
            System.out.print(head.data + " ");
            head = head.next;
        }
    }

    // Driver Code
    public static void main(String[] args)
    {
        Node head = new Node(7);
        Node temp = head;
        temp.next = new Node(10);
        temp = temp.next;
        temp.next = new Node(5);
        temp = temp.next;
        temp.next = new Node(20);
        temp = temp.next;
        temp.next = new Node(3);
        temp = temp.next;
        temp.next = new Node(2);
        temp = temp.next;

        // Apply merge Sort
        head = mergeSort(head);
        System.out.print("\nSorted Linked List is: \n");
        printList(head);
    }
}

Output for merge sort for linked list

Linked List before sorting
8 9 5 3 2 7
Linked List after sorting
2 3 5 7 8 9

Time Complexity: O(n*log n)

So, In this article, we have learned how to merge sort in linked list. We have discussed the merge sort algorithm and also discussed the approaches indicating how we can apply merge sort for sorting linked lists with a complete pictorial dry run. If you want to practice more questions on linked lists feel free to solve them at Prepbytes (Linked Lists).

FAQs for merge sort in linked list

1. Why is merge sort preferred for linked lists?

Merge sort is preferred for linked lists as the nodes may not be present at adjacent locations.

2. What is the time complexity for the merge sort algorithm?

The time complexity for the merge sort algorithm is O(n*logn).

3. Which one is better merge sort or quick sort ?

Merge sort is more suitable, and efficient and works faster than quick sort in larger array sizes.