Last Updated on November 28, 2022 by Prepbytes

This article will discuss the problem partition a linked list around a given value and its proper solution using an algorithm and dry run. Before jumping into the details of the problem and approach to solving it, you need to know about the problem statement of partition a linked list around a given value.
How to partition a linked list around a given value
In this problem, we will be given a linked list and an integer X. We need to partition the linked list around this integer X such that all elements that are less than X should occur before all elements having a value greater than or equal to X.
To understand this problem statement, let us learn programming languages online and take an example.
If the given linked list is:

and X = 5
- Here, X = 5 so, nodes with data less than X are: 1,2,3.
- Nodes with data greater than or equal to X are: 5,8,12.
- We need to keep 1,2,3 before 5,8,12.
- Remember that the order of elements does not matter to us as long as the criteria are satisfied, i.e., elements having a value less than X should be before the elements with a value greater than or equal to X.
- So, the final output will be 1→2→3→5→8→12→NULL
Let us take another example:
If the linked list is 9→1→10→27→42→2→NULL and X = 10
- As explained in the above example, similarly, the output linked list after partitioning the linked list around X = 10 will be: 1→9→2→10→27→42→NULL
Note: The order of the elements does not matter, i.e., in the final linked list, the elements smaller than X should be before the elements greater than or equal to X. The order of the occurrence of the elements in the final linked list need not be the same as the order of occurrence in the initial given linked list. We can change the order of occurrence of elements as long as the main condition is satisfied.
Also, multiple correct outputs are possible for this problem statement.
Now let’s have a look at some helpful observations.
Helpful Observations
- We need to separate the nodes with values less than X from those with values greater than or equal to X.
- The order of occurrence of nodes does not matter to us.
- Multiple correct solutions exist for this problem.
Approach to partition a linked list around a given value
- Here, we will keep track of two pointers i.e., head and tail pointers of the list
- When we encounter an element that is less than X, we will insert it before the head and update the head pointer.
- When we encounter an element greater than or equal to X, we will insert it after the tail node and will update the tail node.
Algorithm to partition a linked list around a given value
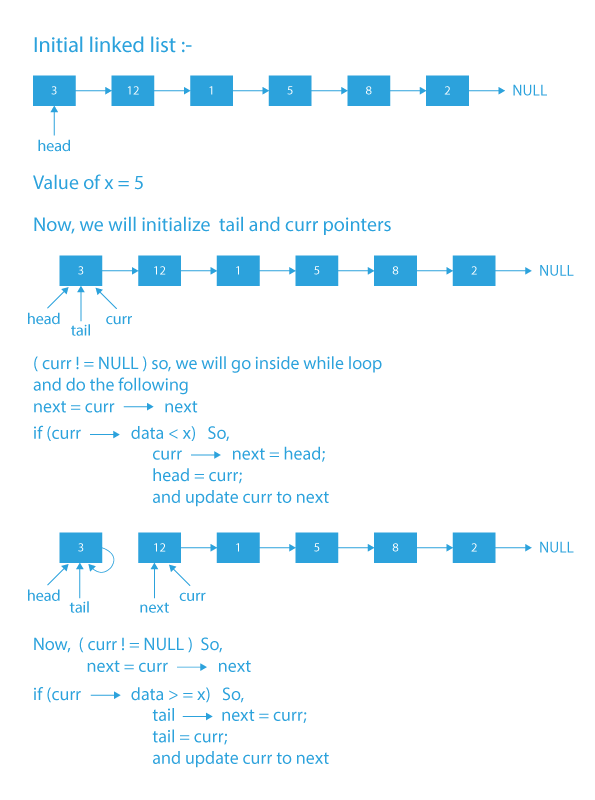
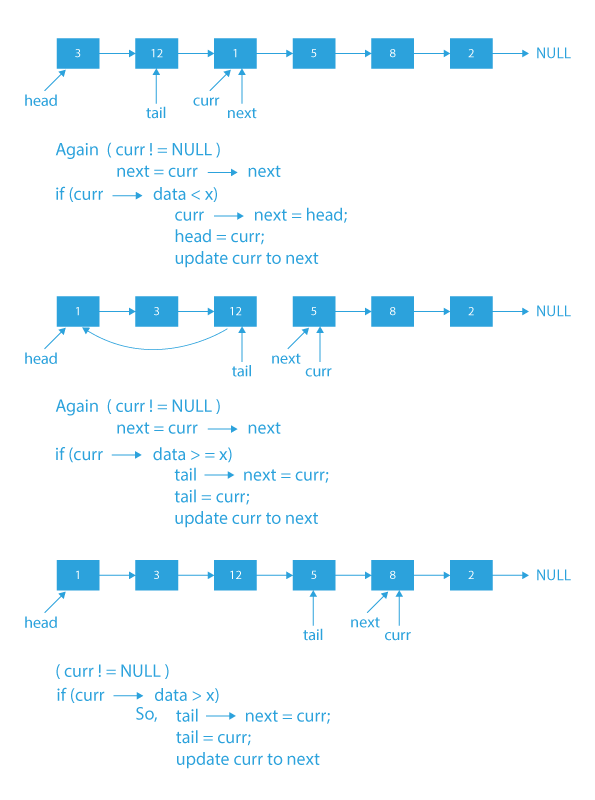
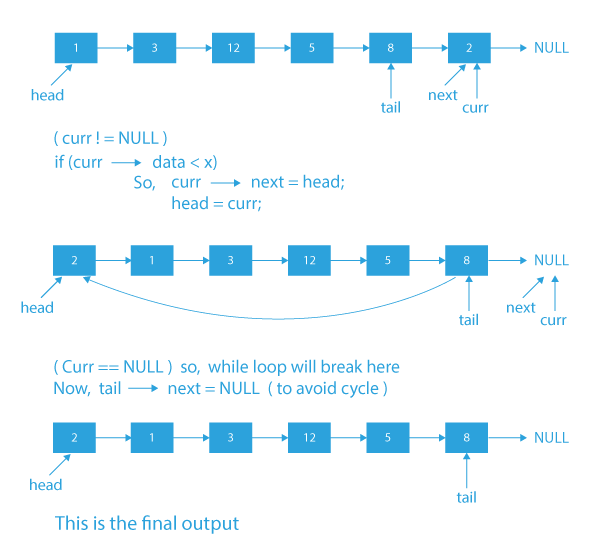
- Initialize two pointers named current and tail with the starting node of the original linked list.
- Loop in the linked list using this pointer current, starting from first to the last node, and store the next pointer of the current node in another variable before inserting the current node before head or after tail.
- If the current node has a value less than X, insert it before head and update the head.
- If the current node has a value greater than or equal to X, insert it after the tail and update the tail pointer.
- Update the current node with the next pointer stored in step 2.
- After the loop ends, make the next pointer of the tail node point to NULL to avoid the cycle in the newly created list.
Dry Run of partition a linked list around a given value
Code Implementation to partition a linked list around a given value
#include<stdio.h>
#include<stdlib.h>
struct Node
{
int data;
struct Node* next;
};
// A utility function to create a new node
Node *newNode(int data)
{
struct Node* new_node = new Node;
new_node->data = data;
new_node->next = NULL;
return new_node;
}
// Function to make a new list(using the existing
// nodes) and return head of new list.
struct Node *partition(struct Node *head, int x)
{
/* Let us initialize start and tail nodes of
new list */
struct Node *tail = head;
// Now iterate original list and connect nodes
Node *curr = head;
while (curr != NULL)
{
struct Node *next = curr->next;
if (curr->data < x)
{
/* Insert node at head. */
curr->next = head;
head = curr;
}
else // Append to the list of greater values
{
/* Insert node at tail. */
tail->next = curr;
tail = curr;
}
curr = next;
}
tail->next = NULL;
// The head has changed, so we need
// to return it to the user.
return head;
}
/* Function to print linked list */
void printList(struct Node *head)
{
struct Node *temp = head;
while (temp != NULL)
{
printf("%d ", temp->data);
temp = temp->next;
}
}
// Driver program to run the case
int main()
{
/* Start with the empty list */
struct Node* head = newNode(3);
head->next = newNode(5);
head->next->next = newNode(8);
head->next->next->next = newNode(2);
head->next->next->next->next = newNode(10);
head->next->next->next->next->next = newNode(2);
head->next->next->next->next->next->next = newNode(1);
int x = 5;
head = partition(head, x);
printList(head);
return 0;
}
#include<bits stdc++.h="">
using namespace std;
class Node
{
public:
int data;
Node* next;
Node(int x){
data = x;
next = NULL;
}
};
Node *partition(Node *head, int x)
{
/* initialize current and tail nodes of new list
as discussed in step 1*/
Node *tail = head;
Node *curr = head;
while (curr != NULL)
{
Node *next = curr->next;
if (curr->data < x) // left partition
{
/* Insert node before head if current node data is
less than given value of X */
curr->next = head;
head = curr; // update the head node
}
else // right partition
{
/* Insert node after tail node */
tail->next = curr;
tail = curr; // update the tail node
}
curr = next;
}
tail->next = NULL; // make next of tail node as NULL to
// avoid cycles in newly created list
// return changed head
return head;
}
void printList(struct Node *head)
{
Node *temp = head;
while (temp != NULL)
{
printf("%d ", temp->data);
temp = temp->next;
}
}
int main(void)
{
Node* head = NULL;
head = new Node(3);
head->next = new Node(12);
head->next->next = new Node(1);
head->next->next->next = new Node(5);
head->next->next->next->next = new Node(8);
head->next->next->next->next->next = new Node(2);
Node *tmp = partition(head,5);
printList(tmp);
return 0;
}
class Partition
{
static class Node
{
int data;
Node next;
}
static Node newNode(int data)
{
Node new_node = new Node();
new_node.data = data;
new_node.next = null;
return new_node;
}
// Function to make a new list
// (using the existing nodes) and
// return head of new list.
static Node partition(Node head, int x)
{
/* Let us initialize start and tail nodes of
new list */
Node tail = head;
// Now iterate original list and connect nodes
Node curr = head;
while (curr != null)
{
Node next = curr.next;
if (curr.data < x)
{
/* Insert node at head. */
curr.next = head;
head = curr;
}
else // Append to the list of greater values
{
/* Insert node at tail. */
tail.next = curr;
tail = curr;
}
curr = next;
}
tail.next = null;
// The head has changed, so we need
// to return it to the user.
return head;
}
static void printList(Node head)
{
Node temp = head;
while (temp != null)
{
System.out.print(temp.data + " ");
temp = temp.next;
}
}
// Driver code
public static void main(String[] args)
{
/* Start with the empty list */
Node head = newNode(3);
head.next = newNode(5);
head.next.next = newNode(8);
head.next.next.next = newNode(2);
head.next.next.next.next = newNode(10);
head.next.next.next.next.next = newNode(2);
head.next.next.next.next.next.next = newNode(1);
int x = 5;
head = partition(head, x);
printList(head);
}
}
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(data):
new_node = Node(data)
new_node.data = data
new_node.next = None
return new_node
# Function to make a new list
# (using the existing nodes)
# and return head of new list.
def partition(head, x):
# Let us initialize start and
# tail nodes of new list
tail = head
# Now iterate original list
# and connect nodes
curr = head
while (curr != None):
next = curr.next
if (curr.data < x):
# Insert node at head.
curr.next = head
head = curr
else:
# Append to the list of greater values
# Insert node at tail.
tail.next = curr
tail = curr
curr = next
tail.next = None
# The head has changed, so we need
# to return it to the user.
return head
# Function to print linked list
def printList(head):
temp = head
while (temp != None):
print(temp.data, end = " ")
temp = temp.next
# Driver Code
if __name__=='__main__':
# Start with the empty list
head = newNode(3)
head.next = newNode(12)
head.next.next = newNode(1)
head.next.next.next = newNode(5)
head.next.next.next.next = newNode(8)
head.next.next.next.next.next = newNode(2)
x = 5
head = partition(head, x)
printList(head)
Output
2 1 3 12 5 8Time Complexity: O(n), Where n is the number of nodes in the list.
This article discusses how you can partition a linked list around a given value without caring about maintaining the stability in elements of the list in the most optimal way. We have discussed the most-efficient approach to solve the problem, and discussed the time and space complexities. If you want to solve more questions on Linked List, which is curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs related to partition a linked list around a given value
1. What is a linked list?
A linked list is a linear data structure that is formed by a collection of connected nodes. Each node consists of data and a pointer to the next node.
2. State the main difference between a singly linked list and a doubly linked list?
A singly-linked list is unidirectional, which means that the node of a singly-linked list contains the pointer to its next node only. In contrast, a doubly-linked list is bidirectional, and its node contains the pointer to its next and previous nodes.
3. How do you split a linked list?
- Store the mid and last pointers of the circular linked list using the tortoise and hare algorithm.
- Make the second half circular.
- Make the first half circular.
- Set head (or start) pointers of the two linked lists.


