Reverse A Sublist Of Linked List

Last Updated on November 27, 2023 by Ankit Kochar

Manipulating linked lists is a core skill for programmers working with data structures. Among the numerous operations, reversing a sublist within a linked list presents an intriguing challenge. This article delves into the intricacies of reversing a sublist in a linked list data structure. Understanding this operation not only showcases a grasp of linked list manipulation but also demonstrates proficiency in algorithmic thinking and problem-solving. Given a linked list and two integers (say ‘m’ and ‘n’). We need to reverse the list from position m to n and leave the rest of the list as it is.

How To Reverse a Sublist of Linked List?

Let’s try to understand this problem with the help of examples.

If the list given to us is:

• According to the problem statement, we need to reverse the given list from position m=3 to position n=5, i.e., from 3^rd node to 5^th node (both inclusive).
• The sublist from position 3 to position 5 is 1→7→4, so we need to reverse this sublist of the given linked list.
• Our final output linked list after reversing the sublist is:

Let’s take another example, let the input be 9→4→8→7→1→NULL, m = 2, n = 3.

• So in this case, after reversing the sublist from position 2 to 3 (both inclusive), our final output list will be 9→8→4→7→1→NULL.

Some more examples

Sample Input 1: 1→3→5→7→9→11→13→NULL, m = 2, n = 4
Sample Output 1: 1→7→5→3→9→11→13→NULL

Sample Output 2: 1→2→5→6→4→8→NULL, m = 2, n = 6
Sample Output 2: 1→8→4→6→5→2→NULL

Now, I think from the above examples, the problem statement is clear. Let’s see how we can approach it.

Before moving to the approach section, try to think about how you can approach this problem.
If stuck, no problem, we will thoroughly see how we can approach this problem in the next section.

Let’s move to the approach section.

Approach

Our approach will be quite straightforward.

• At first, we need to find the m^th node.
• Then we find the n^th node.
• After that, we need to detach the list that is present after the n^th node and save the (n+1)^th node’s address in a variable.
• Then we need to reverse the sublist starting from the m^th node to the n^{th node.}
• Now, we need to attach this reversed list after (m-1)^th node and also attach the remaining list whose address we stored in a temporary variable after the n^th node.

Following these steps will give us the required answer.

Algorithm

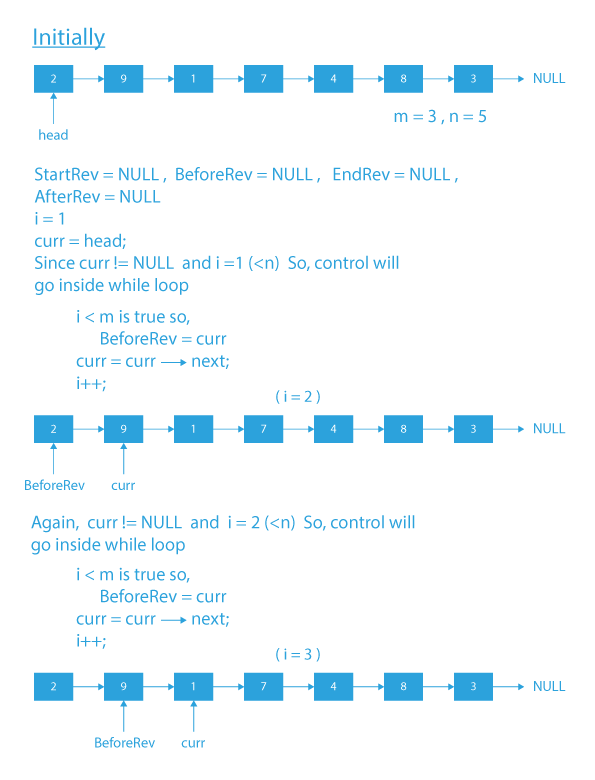
• Initialize four pointers named StartRev, BeforeRev, EndRev, AfterRev with NULL and an integer variable i with 1.
• Initialize a curr variable with the head pointer for iteration of the list.
• Now, run a while loop till curr reaches NULL, and i is less than n.
• Inside the while loop:
  • If i is less than m, update BeforeRev with curr.
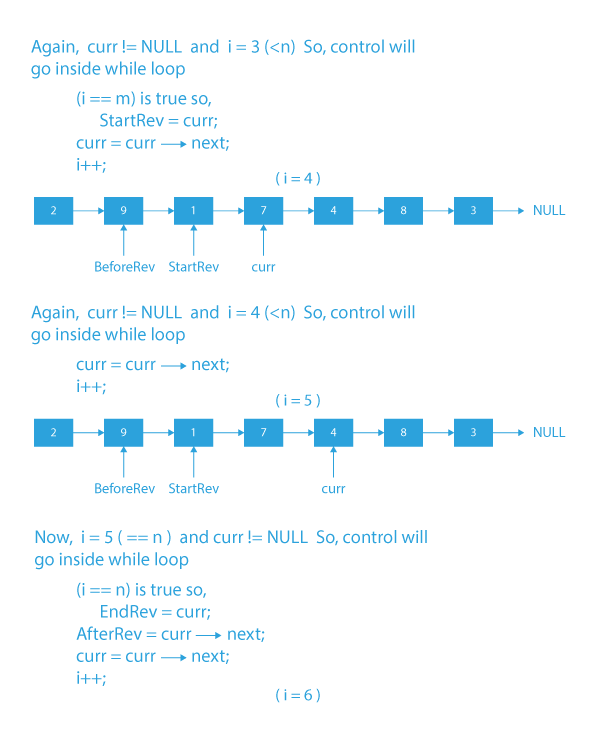
  • If i is equal to m, update StartRev with curr.
  • If i is equal to n, update EndRev with curr and AfterRev with curr->next.
  • Increment i by 1.
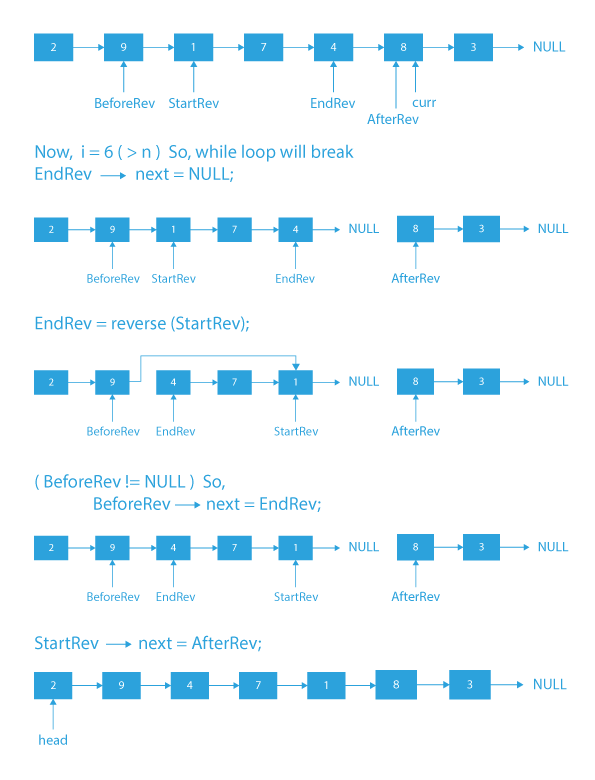
• Make EndRev->next as NULL to detach the list after the m^th node.
• Now, reverse the list with StartRev as starting node.
• Check if BeforeRev is NULL or not:
  • If it is not NULL, then assign BeforeRev->next to EndRev.
  • Else update head with EndRev.
• Assign StartRev->next with AfterRev.
• Return the head pointer.

If you are not aware of how to reverse a linked list, please check this article Reversing a linked list.

Dry Run

Code Implementation:

#include <stdio.h>
#include <stdlib.h>
 
// Linked list node
struct Node {
    int data;
    struct Node* next;
};
 
// the standard reverse function used
// to reverse a linked list
struct Node* reverse(struct Node* head)
{
    struct Node* prev = NULL;   
    struct Node* curr = head;
 
    while (curr) {
        struct Node* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}
 
// function used to reverse a linked list
// from position m to n which uses reverse
// function
struct Node* reverseBetween(struct Node* head, int m, int n)
{
    if (m == n)
        return head;
 
    // revs and revend is start and end respectively
    // of the portion of the linked list which
    // need to be reversed. revs_prev is previous
    // of starting position and revend_next is next
    // of end of list to be reversed.
    struct Node* revs = NULL, *revs_prev = NULL;
    struct Node* revend = NULL, *revend_next = NULL;
 
    // Find values of above pointers.
    int i = 1;
    struct Node* curr = head;
    while (curr && i <= n) {
        if (i < m)
            revs_prev = curr;
 
        if (i == m)
            revs = curr;
 
        if (i == n) {
            revend = curr;
            revend_next = curr->next;
        }
 
        curr = curr->next;
        i++;
    }
    revend->next = NULL;
 
    // Reverse linked list starting with
    // revs.
    revend = reverse(revs);
 
    // If starting position was not head
    if (revs_prev)
        revs_prev->next = revend;
 
    // If starting position was head
    else
        head = revend;
 
    revs->next = revend_next;
    return head;
}
 
void print(struct Node* head)
{
    while (head != NULL) {
        printf("%d ", head->data);
        head = head->next;
    }
    printf("\n");
}
 
// function to add a new node at the
// beginning of the list
void push(struct Node** head_ref, int new_data)
{
    struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
    new_node->data = new_data;
    new_node->next = (*head_ref);
    (*head_ref) = new_node;
}
 
// Driver code
int main()
{
    struct Node* head = NULL;
    push(&head, 7);
    push(&head, 6);
    push(&head, 5);
    push(&head, 4);
    push(&head, 3);
    push(&head, 2);
    push(&head, 1);
    reverseBetween(head, 2, 4);
    print(head);
    return 0;
}

#include <bits/stdc++.h>
using namespace std;

/* Node structure of a singly linked list */
class Node {
    public:
    int data;
    Node* next;
    Node(int x){
        data = x;
        next = NULL;
}
};

/* Using this function we will be printing the linked list */
void printingList(Node* head)
{
    Node* curr = head;
    while (curr != NULL) {
        cout << curr->data << " -> ";
        curr = curr->next;
    }
    cout<<"NULL";
    cout<<endl;
}

/* Using this function we will be reversing a linked list whose head pointer is given */
Node* reverseList(Node* head)
{
    Node* prev = NULL;   
    Node* curr = head;
 
    while (curr) {
        Node* next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}
 
/* Using this function we will be reversing the sublist from mth till nth position */
Node* ReverseFromMToN(Node* head, int m, int n)
{
    if (m == n)
        return head;

    Node* StartRev = NULL, *BeforeRev = NULL;
    Node* EndRev = NULL, *AfterRev = NULL;
 
    int i = 1;
    Node* curr = head;
    while (curr && i <= n) {
        if (i < m)
            BeforeRev = curr;
 
        if (i == m)
            StartRev = curr;
 
        if (i == n) {
            EndRev = curr;
            AfterRev = curr->next;
        }
 
        curr = curr->next;
        i++;
    }
    
    EndRev->next = NULL;
 
    EndRev = reverseList(StartRev);
 
    if (BeforeRev)
        BeforeRev->next = EndRev;

    else
        head = EndRev;
    
    StartRev->next = AfterRev;
 
    return head;
}

int main()
{
    Node *head = new Node(2);
    head->next = new Node(9);
    head->next->next = new Node(1);
    head->next->next->next = new Node(7);
    head->next->next->next->next = new Node(4);
    head->next->next->next->next->next = new Node(8);
    head->next->next->next->next->next->next = new Node(3);
    cout<<"Original given linked list before reversing sublist:"<<endl;
    printingList(head);
    head = ReverseFromMToN(head, 3, 5);
    cout<<"Linked list after reversing sublist:"<<endl;
    printingList(head);
    return 0;
}

class Node:
	
	def __init__(self, data):
		
		self.data = data
		self.next = None

def reverse(head):

	prev = None
	curr = head

	while (curr):
		next = curr.next
		curr.next = prev
		prev = curr
		curr = next
	
	return prev

def reverseBetween(head, m, n):

	if (m == n):
		return head
		
	revs = None
	revs_prev = None
	revend = None
	revend_next = None

	i = 1
	curr = head
	
	while (curr and i <= n):
		if (i < m):
			revs_prev = curr

		if (i == m):
			revs = curr

		if (i == n):
			revend = curr
			revend_next = curr.next

		curr = curr.next
		i += 1

	revend.next = None

	revend = reverse(revs)

	if (revs_prev):
		revs_prev.next = revend

	else:
		head = revend

	revs.next = revend_next
	return head

def prints(head):

	while (head != None):
		print(head.data, end = ' ')
		head = head.next
		
	print()

def push(head_ref, new_data):

	new_node = Node(new_data)
	new_node.data = new_data
	new_node.next = (head_ref)
	(head_ref) = new_node
	return head_ref

if __name__=='__main__':
	
	head = None
	head = push(head, 3)
	head = push(head, 8)
	head = push(head, 4)
	head = push(head, 7)
	head = push(head, 1)
	head = push(head, 9)
	head = push(head, 2)
	
	reverseBetween(head, 3, 5)
	
	prints(head)

Output

Original given linked list before reversing sublist:
2 -> 9 -> 1 -> 7 -> 4 -> 8 -> 3 -> NULL
Linked list after reversing sublist:
2 -> 9 -> 4 -> 7 -> 1 -> 8 -> 3 -> NULL

Time Complexity: O(n), n is the number of nodes present in the list
[forminator_quiz id=”5041″]

**Conclusion**
Reversing a sublist within a linked list is a valuable skill that demonstrates adeptness in linked list manipulation and algorithmic problem-solving. Understanding the intricacies of identifying the sublist, manipulating pointers, and ensuring efficient traversal aids in mastering this operation. Proficiency in this fundamental operation contributes to a programmer’s ability to efficiently manage and manipulate linked list data structures, unlocking potential applications across diverse domains in computer science and software development.

## FAQ: Reversing a Sublist of a Linked List
Here are some FAQs related to how to reverse a Sublist of Linked List.

**1. What does “reversing a sublist of a linked list” mean?**
Reversing a sublist in a linked list involves altering the order of elements within a specified range. For instance, given a linked list with nodes 1 -> 2 -> 3 -> 4 -> 5 and a sublist specified from positions 2 to 4, the resulting list after reversal would be 1 -> 4 -> 3 -> 2 -> 5.

**2. How is a sublist reversal operation performed on a linked list?**
To reverse a sublist in a linked list, the algorithm typically involves traversing the list to find the starting and ending nodes of the sublist. Then, the nodes within the sublist are reversed by changing the pointers, effectively altering their order.

**3. What are the key challenges when reversing a sublist in a linked list?**
Ensuring accurate identification of the starting and ending points of the sublist is crucial. Moreover, handling cases where the sublist begins at the head or ends at the tail of the linked list requires special consideration in pointer manipulation.

**4. Can reversing a sublist be achieved in constant space complexity?**
Reversing a sublist usually requires linear space complexity due to the traversal and temporary storage of nodes. However, in-place reversal techniques can be employed to minimize space usage, where pointers are adjusted without extra memory allocation.

**5. What are the applications of reversing sublists in linked lists?**
Reversing sublists within linked lists finds applications in various algorithms and data manipulation tasks, such as in competitive programming challenges, string and list manipulations in software development, and specific tasks in database management systems.