Last Updated on November 18, 2022 by Prepbytes

We are already aware about how a linked list stores elements in a non-contiguous manner and still connects all the elements via links. Therefore, we will discuss how to find length of linked list and one should be aware of how many elements are present in the linked list to perform any kind of operation. So let’s just see how to find length of linked list.
Problem statement for linked list length
Given a singly linked list, find its length.
Input:

Output: 4.
As there are 4 nodes in the linked list.
Input:

Output: 0.
As there is no node in the linked list.
How do we define the length of a linked list?
The length of a linked list is the total number of nodes in it.
Approach (Iterative) to find length of linked list
We know how to iterate through the linked list. In an iteration, we visit each node exactly once. We can keep track of the count of each node visited and that will be the length of the linked list.
Algorithm to find length of linked list
- Initialize answer as 0.
- Iterate through the linked list and for each iteration increment the answer by 1.
- After the iteration completes, return the answer.
Implementation:
#include<stdio.h>
#include<stdlib.h>
/* Link list node */
struct Node
{
int data;
struct Node* next;
};
/* Given a reference (pointer to pointer) to the head
of a list and an int, push a new node on the front
of the list. */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Counts no. of nodes in linked list */
int getCount(struct Node* head)
{
int count = 0; // Initialize count
struct Node* current = head; // Initialize current
while (current != NULL)
{
count++;
current = current->next;
}
return count;
}
/* Driver program to test count function*/
int main()
{
/* Start with the empty list */
struct Node* head = NULL;
/* Use push() to construct below list
1->2->1->3->1 */
push(&head, 1);
push(&head, 3);
push(&head, 1);
push(&head, 2);
push(&head, 1);
/* Check the count function */
printf("count of nodes is %d", getCount(head));
return 0;
}
#include<bits/stdc++.h>
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
// function to find length of a linked list
int length_iterative(Node* head){
int answer = 0;
for(Node* i=head;i!=NULL;i=i->next){
answer ++;
}
return answer;
}
int main(){
Node *head = NULL;
push_front(&head, 10);
push_front(&head, 3);
push_front(&head, 7);
push_front(&head, 2);
cout<<length_iterative(head)<<"\n";
}
class Node
{
int data;
Node next;
Node(int d) { data = d; next = null; }
}
class Length
{
Node head;
public void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
public int getCount()
{
Node temp = head;
int count = 0;
while (temp != null)
{
count++;
temp = temp.next;
}
return count;
}
public static void main(String[] args)
{
Length llist = new Length();
llist.push(1);
llist.push(3);
llist.push(1);
llist.push(2);
llist.push(1);
System.out.println("Count of nodes is " +llist.getCount());
}
}
class Node: def __init__(self, data): self.data = data self.next = None class LinkedList: def __init__(self): self.head = None def push(self, new_data): new_node = Node(new_data) new_node.next = self.head self.head = new_node def getCount(self): temp = self.head count = 0 while (temp): count += 1 temp = temp.next return count if __name__=='__main__': llist = LinkedList() llist.push(10) llist.push(3) llist.push(7) llist.push(2) print (llist.getCount())
Output
4
Time complexity: O(n), since we are traversing the linked list once.
Space complexity: O(1), as we aren’t using any extra space.
Here, ‘n’ is the number of nodes in the linked list.
Approach (Recursive) to find length of linked list
To solve this problem recursively, we need to break this problem down into subproblems as we do in all recursive approaches.
For a given node of a linked list, we know it will contribute 1 to the total length. So, now we need to find the length of the linked list following the current node and add 1 to it. Finding the length of the remaining list can be seen as the same problem and hence can be solved by calling the same function for the next node.
So, the length of a linked list with ‘head’ as a pointer to 1st node can be written as: length(head) = 1 + length(head->next)
The length will be 0 for an empty linked list. This can be used as the base case in our recursive function.
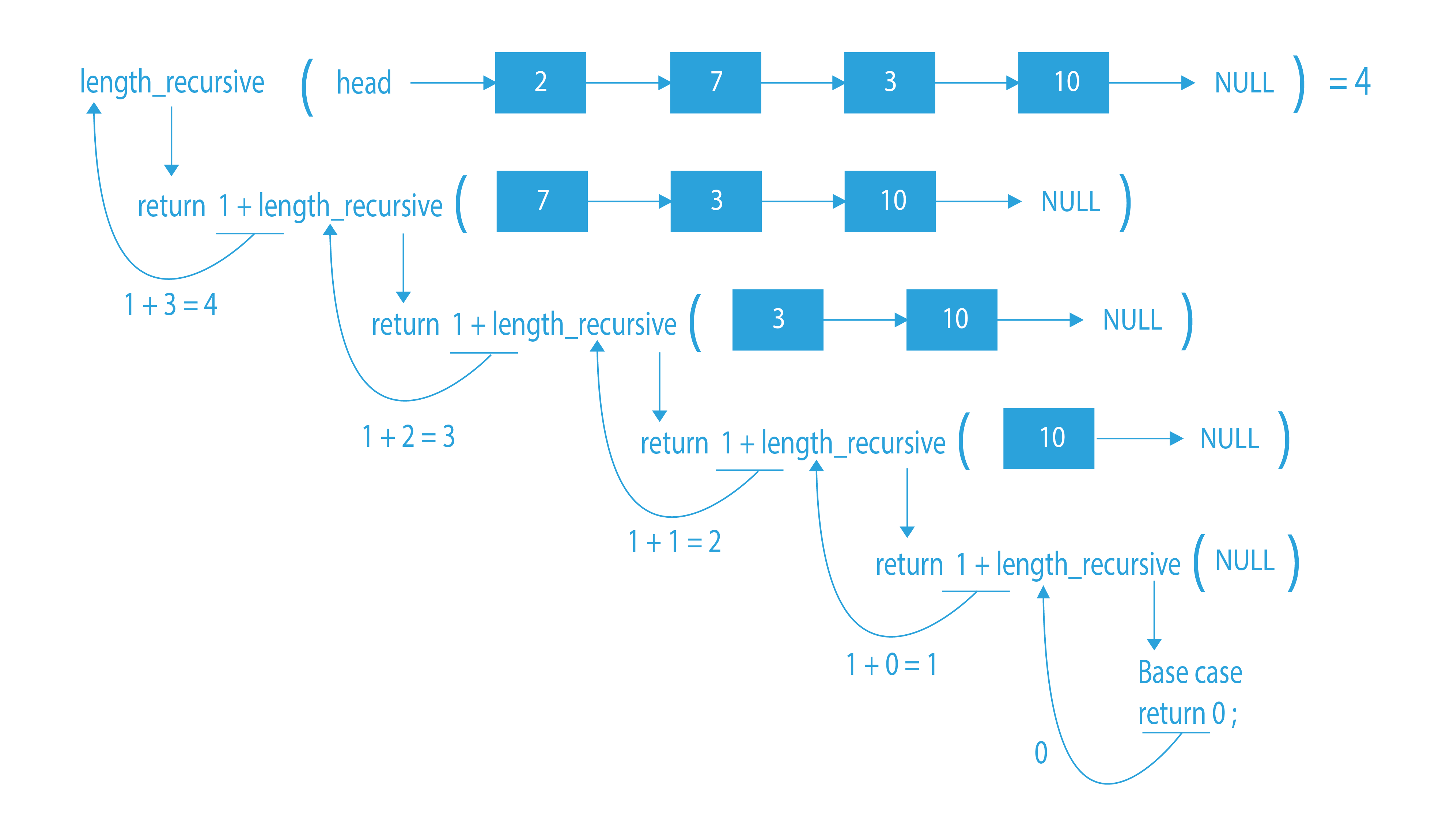
Since it is clear what we need to do, take some time and think about how we are going to do it.
Algorithm for linked list length
- If head points to NULL, return 0. (base case)
- Else recursively call the same function for head->next and add 1 to its result.
- Return the answer.
Implementation to find length of linked list
#include<stdio.h>
#include<stdlib.h>
/* Link list node */
struct Node
{
int data;
struct Node* next;
};
/* Given a reference (pointer to pointer) to the head
of a list and an int, push a new node on the front
of the list. */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node =
(struct Node*) malloc(sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list off the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
int getCount(struct Node* head)
{
// Base Case
if (head == NULL) {
return 0;
}
// Count this node plus the rest of the list
else {
return 1 + getCount(head->next);
}
}
/* Driver program to test count function*/
int main()
{
/* Start with the empty list */
struct Node* head = NULL;
/* Use push() to construct below list
1->2->1->3->1 */
push(&head, 1);
push(&head, 3);
push(&head, 1);
push(&head, 2);
push(&head, 1);
/* Check the count function */
int ans = getCount(head);
printf("Count of nodes is %d",ans);
return 0;
}
#include<bits/stdc++.h>
using namespace std;
struct Node {
int val;
Node* next;
Node(int value){
val = value;
next = NULL;
}
};
void push_front(Node** head, int new_val){
Node* new_node = new Node(new_val);
new_node->next = *head;
*head = new_node;
}
int length_recursive(Node* head){
if(head==NULL) return 0;
return 1 + length_recursive(head->next);
}
int main(){
Node *head = NULL;
push_front(&head, 10);
push_front(&head, 3);
push_front(&head, 7);
push_front(&head, 2);
cout<<length_recursive(head);
}
class Node
{
int data;
Node next;
Node(int d) { data = d; next = null; }
}
class LengthRecursive
{
Node head;
public void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
public int getCountRec(Node node)
{
if (node == null)
return 0;
return 1 + getCountRec(node.next);
}
public int getCount()
{
return getCountRec(head);
}
public static void main(String[] args)
{
LengthRecursive llist = new LengthRecursive();
llist.push(1);
llist.push(3);
llist.push(1);
llist.push(2);
llist.push(1);
System.out.println("Count of nodes is " +llist.getCount());
}
}
Output
4
Time complexity of linked list length: O(n), as we are completely traversing the linked list once.
Space complexity of linked list length: O(n), due to recursive function call stack.
Here ‘n’ is the number of nodes in the linked list.
Conclusion
Through this article, we learned how to find the length of linked list using both iterative and recursive methods. We have also tried to understand how knowing the length of linked list is important. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs
- What is the space complexity of the length of linked list?
- Why is arraylist slower than linked list?
A linked list contains a node which has two parts, so it is known that the space increases as the elements increase. Hence the space complexity for the length of linked list is O(n).
Arraylist works and implements exactly as an array which is slow whereas the linked list implements through the node and pointers which require less shifting.


