Last Updated on November 16, 2022 by Prepbytes

In the respective article, we will look how stable sorting such as insertion sort works in doubly linked lists. Now let’s just see an approach of insertion sort for doubly linked list.
Problem Statement of doubly linked list insertion sort
In this question, we are given a doubly linked list. We have to sort the given list using the insertion sort technique.
Input:
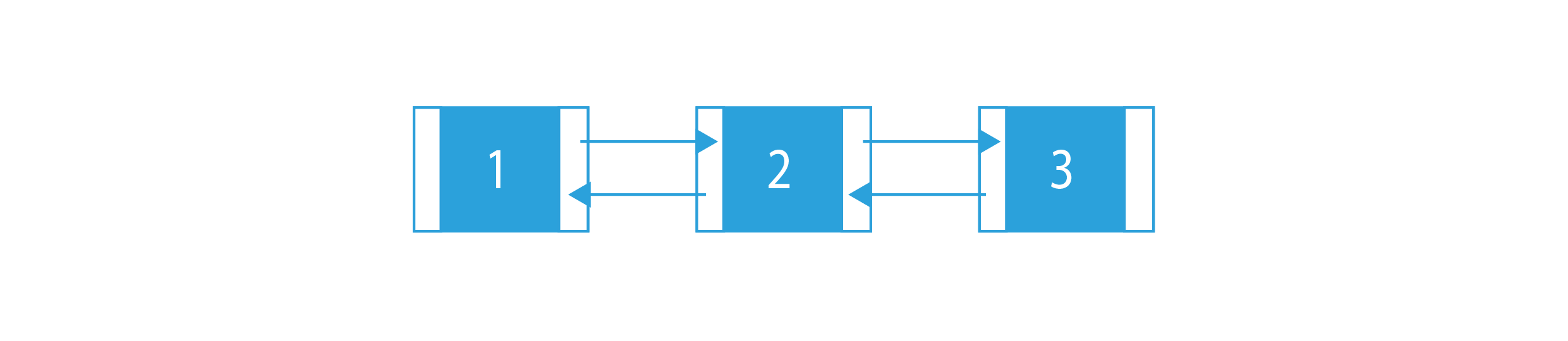
Output:
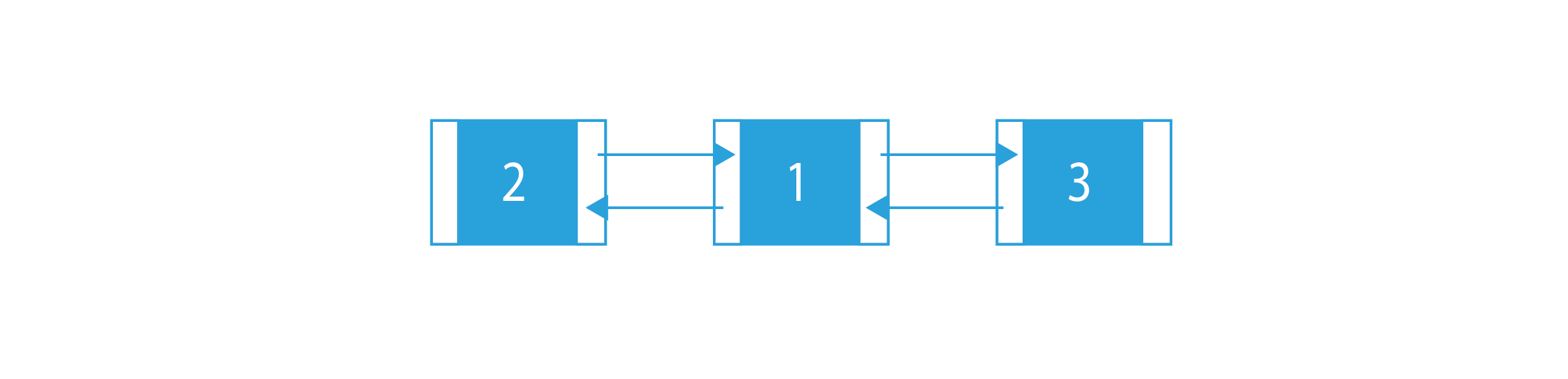
Explanation: The given list has been sorted.
This question is not a tricky one. We just have to extract the elements from the list one by one, and insert them in the new list in a sorted way. This sorted insert technique has been explained in detail in the approach.
Let us have a glance at the approach.
Approach of insertion sort for doubly linked list
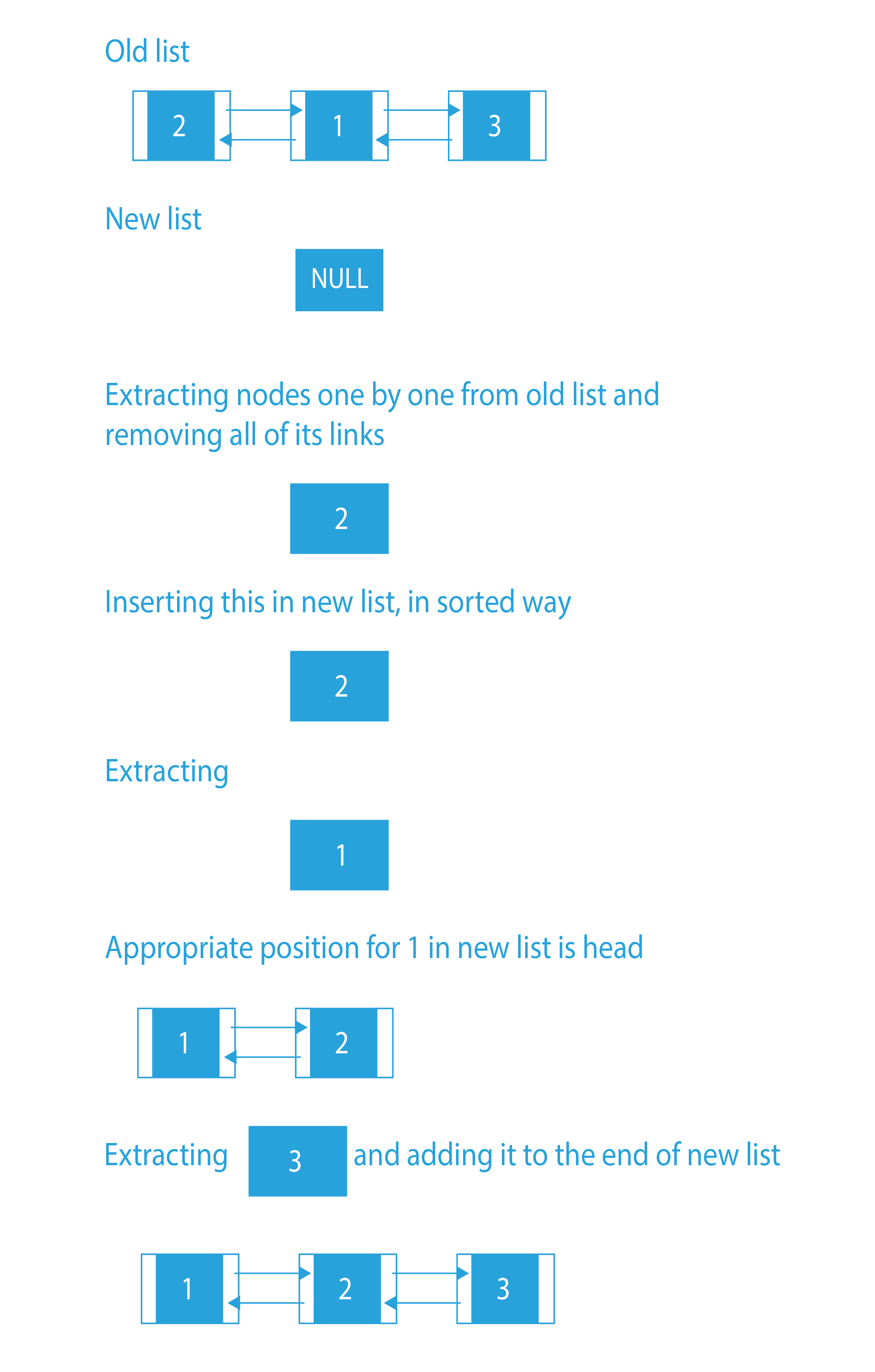
The approach is going to be pretty simple. We will create an empty result doubly linked list which will be sorted. Then, we will traverse the given doubly linked list, and for every node that we visit, we will insert the current node in a sorted way in our result list.
To insert in a sorted way, we will traverse our result list and keep comparing every node with our current node. As soon as we find a node whose value is greater than the current node, we will insert the current node just before that node. If the current node value is greater than every other node of our result list, then we will append the current node at the end.
After complete traversal, change the head of the given linked list to the head of the result list.
Algorithm of doubly linked list insertion sort
- Initialize the newly created sorted list as NULL.
- Traverse the given doubly linked list.
- For every node, store the next of node in a temp variable and remove all of its links.
- Insert the current node in a sorted way in the result list.
- To insert in a sorted way, traverse through the result list and keep comparing every node with our current node. As soon as a node is found whose value is greater than the current node, we will insert the current node just before that node. If the current node value is greater than every node of the result list, then append the current node at the end of the result list.
- Update current’s value with temp.
- Update the head pointer by making it point to our result list.
Dry Run of insertion sort for doubly linked list
Code Implementation of doubly linked list insertion sort
#includeusing namespace std; struct Node { int data; struct Node* prev, *next; }; struct Node* getNode(int data) { struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); newNode->data = data; newNode->prev = newNode->next = NULL; return newNode; } // Function to insert in a sorted way void sortedInsert(struct Node** head_ref, struct Node* newNode) { struct Node* current; // if the list is empty if (*head_ref == NULL) *head_ref = newNode; // if the node is to be inserted at the start // of the sorted doubly linked list else if ((*head_ref)->data >= newNode->data) { newNode->next = *head_ref; newNode->next->prev = newNode; *head_ref = newNode; } else { current = *head_ref; // find the node after which the new node // is to be inserted while (current->next != NULL && current->next->data < newNode->data) current = current->next; /*Make the appropriate links */ newNode->next = current->next; // if the new node is not inserted at the // end of the sorted doubly linked list if (current->next != NULL) newNode->next->prev = newNode; current->next = newNode; newNode->prev = current; } } // Function to sort the doubly linked list // using insertion sort void insertionSort(struct Node** head_ref) { // Initialize sorted doubly linked list with NULL struct Node* sorted = NULL; // Traverse through the given list struct Node* current = *head_ref; while (current != NULL) { // Store next for next iteration struct Node* next = current->next; // Rremovee all the links current->prev = current->next = NULL; // insert current in the 'sorted' doubly linked list sortedInsert(&sorted, current); // Update current current = next; } // Update the head *head_ref = sorted; } void printList(struct Node* head) { while (head != NULL) { cout << head->data << " "; head = head->next; } } void push(struct Node** head_ref, int new_data) { struct Node* new_node = (struct Node*)malloc(sizeof(struct Node)); new_node->data = new_data; new_node->next = (*head_ref); new_node->prev = NULL; if ((*head_ref) != NULL) (*head_ref)->prev = new_node; (*head_ref) = new_node; } int main() { struct Node* head = NULL; push(&head, 2); push(&head, 1); push(&head, 3); cout << "Doubly Linked List Before Sorting \n"; printList(head); insertionSort(&head); cout << "\n Doubly Linked List After Sorting \n"; printList(head); return 0; }
public class Solution
{
static class Node
{
int data;
Node prev, next;
};
static Node getNode(int data)
{
Node newNode = new Node();
newNode.data = data;
newNode.prev = newNode.next = null;
return newNode;
}
static Node sortedInsert(Node head_ref, Node newNode)
{
Node current;
if (head_ref == null)
head_ref = newNode;
else if ((head_ref).data >= newNode.data)
{
newNode.next = head_ref;
newNode.next.prev = newNode;
head_ref = newNode;
}
else
{
current = head_ref;
while (current.next != null &&
current.next.data < newNode.data)
current = current.next;
newNode.next = current.next;
if (current.next != null)
newNode.next.prev = newNode;
current.next = newNode;
newNode.prev = current;
}
return head_ref;
}
static Node insertionSort(Node head_ref)
{
Node sorted = null;
Node current = head_ref;
while (current != null)
{
Node next = current.next;
current.prev = current.next = null;
sorted=sortedInsert(sorted, current);
current = next;
}
head_ref = sorted;
return head_ref;
}
static void printList(Node head)
{
while (head != null)
{
System.out.print(head.data + " ");
head = head.next;
}
}
static Node push(Node head_ref, int new_data)
{
Node new_node = new Node();
new_node.data = new_data;
new_node.next = (head_ref);
new_node.prev = null;
if ((head_ref) != null)
(head_ref).prev = new_node;
(head_ref) = new_node;
return head_ref;
}
public static void main(String args[])
{
Node head = null;
head=push(head, 2);
head=push(head, 1);
head=push(head, 3);
System.out.println( "Doubly Linked List Before Sorting\n");
printList(head);
head=insertionSort(head);
System.out.println("\nDoubly Linked List After Sorting\n");
printList(head);
}
}
Output
Doubly Linked List Before Sorting
2 1 3
Doubly Linked List After Sorting
1 2 3
Time Complexity of doubly linked list insertion sort: O(n2), as we are using nested traversal.
Conclusion
So, in this article, we have tried to explain the most efficient approach of Insertion sort for doubly linked list. Insertion sort is an important technique, and when it gets coupled with a doubly linked list, it becomes even more important. If you want to solve more questions on Linked List, which are curated by our expert mentors at PrepBytes, you can follow this link Linked List.
FAQs of insertion sort for doubly linked list
- Why insertion sort is called a stable sorting?
- Why is doubly linked list is preferred than singly linked list?
- What is the time complexity of doubly linked list?
Because in insertion sort for doubly linked list two equivalent items will always be preserved.
As doubly linked list is also a two way list, so the implementation of doubly linked list is way more easier than a singly linked list.
The time complexity of doubly linked list is O(1).


