Python Program to find the middle of a linked list using only one traversal

Python program for middle element of linked list, how to find middle element of linked list in python.

Introduction

We can define a linked list as a sequence of elements which are basically connected through links. We have different kinds of operations such as insertion, deletion and searching, let’s just look into one of the searches which is for middle element. Lets just try to understand a Python program for middle element of linked list

Problem Statement on how to find middle element of linked list in python

In this problem, we are given a singly linked list. We have to find the middle of the linked list in a single traversal.

Problem Statement Understanding for Python program for middle element of linked list

Usually, whenever we find the middle of a linked list, 2 traversals are needed.

• 1^st traversal to find the length of the list.
• 2^nd traversal to reach the (length/2)^th node of the list which is actually the middle node of the linked list.

But here we have to find the middle of the linked list in one traversal.

Suppose the given list is 5 → 10 → 15 → 4 → 8. The middle of the list will be 15.

Input :

Output : 15

Explanation: The middle of the given list is 15.

As stated in the problem statement, we have to find the middle of the list in a single traversal. How can we tackle this?

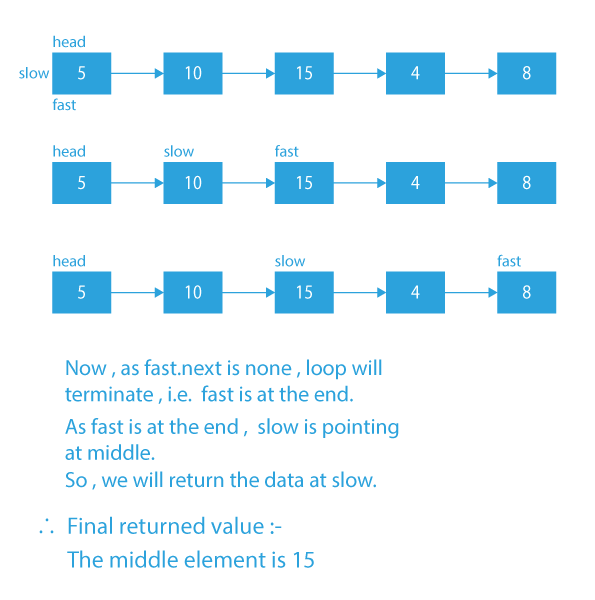
• What if we start by taking two pointers, say slow and fast, and make both of them point to the head initially.
• Now, what will happen if we make the slow jump one place and the fast jump two places (fast moving with twice the speed of slow).
• If we notice carefully, by doing the above step, when the fast will reach the end of the list, the slow will be pointing to the middle of the list.
• With the help of this technique, we can reach the middle node of a linked list in a single pass and hence our objective of finding the middle of linked list in one traversal will be achieved.

The reason why our slow pointer will be pointing to the middle of the linked list when our fast pointer is at end is that, as our slow pointer is travelling with half the speed of fast pointer so when the fast pointer will reach the end of the linked list, till that time slow pointer should have only travelled half the distance as travelled by fast pointer and hence it will be at the middle of the linked list.

Do you know what the above-explained method is called?

This above approach is called the slow and fast pointer method. The slow and fast pointer method has been explained in detail in the approach section and in the dry run.

Let us have a glance at the approach.

Approach for Python program for middle element of linked list

Let us see what the slow and fast pointer technique is:

Initially, both the slow and fast pointer will point to the head of the linked list. Then, we will move both of the pointers slow and fast until fast reaches the end. The fast pointer will jump two places, whereas the slow pointer will one place.

When the fast pointer will reach the end of the linked list, the slow pointer will be pointing to the middle of the linked list.

Algorithm on how to find middle element of linked list in python

• Create two pointers slow and fast.
• Initially both slow and fast will be pointing to the head of the list.
• Now, make the slow pointer jump one place and the fast pointer jump two places until fast reaches the end of the list.
• When the fast pointer reaches the end of the list, the slow pointer will be pointing to the middle of the list.
• In the end, return the data of the slow pointer, as the slow will be pointing to the middle of the list.

Dry Run for Python program for middle element of linked list

Code Implementation for how to find middle element of linked list in python

class Node:

    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:

    def __init__(self):
        self.head = None

    def push(self, new_data):
        new_node = Node(new_data)
        new_node.next = self.head
        self.head = new_node

    def printMiddle(self):
        slow_ptr = self.head
        fast_ptr = self.head

        if self.head is not None:
            while (fast_ptr is not None and fast_ptr.next is not None):
                fast_ptr = fast_ptr.next.next
                slow_ptr = slow_ptr.next
            print("The middle element is: ", slow_ptr.data)

list1 = LinkedList()
list1.push(8)
list1.push(4)
list1.push(15)
list1.push(10)
list1.push(5)
list1.printMiddle()

Output

The middle element is: 15

Time Complexity for Python program for middle element of linked list: O(n), as list traversal is needed.

In the above article we have tried to explain the most efficient approach to find the middle of a linked list using a single traversal. Here we have first explained the probem statement followed by different approaches having dry run in a pictorial representation and also provided the code implementation as well. If you want to brush up your skills on a linked list,you can follow this link Linked List.

FAQs for Python program for middle element of linked list

1. How do you find the middle of a string in python?

With centre () method, we can find the middle of a string in python.

2. What does slice() do in python?

The slice() returns an object means you can specify where to start from slicing and where to end.

3. Can you slice a list in python?

Python supports slice notation for any sequential data type like tuples,bytes,bytearrays, strings, lists and ranges.